|
|||||||||||||||||||||||||||||||||||
![]()
|
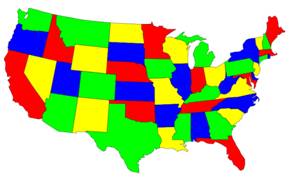
Théorèmes des quatre couleurs Ou problème de Gunthrie Historique
Premier questionnement en
1852 à propos de la coloration des cantons anglais. Résolution en 1976 avec
l'aide d'un ordinateur pour explorer systématiquement les 1500 cas
récalcitrants. Pour résoudre ce problème
qui semblait simple, il a fallu attendre que la puissance de calcul des
ordinateurs soit disponible. |
Américain: The four color problem ot the 4-color theorem (4CT) or the
Gunthrie's problem
|
|
|||
|
Comme
souvent pour les problèmes les plus ardus, la démonstration correspond à une
succession de procédés permettant de reporter la démonstration générale dans
un autre monde et, comme cela, de rebond en rebond, aboutir à la solution
finale. Historique |
|||
|
/ |
/ |
|
|
|
1750 |
Leonhard
Euler (1717-1783)
|
|
|
|
1794 |
Adrien-Marie
Legendre (1752-1833) |
|
|
|
1811 |
Simon-Antoine
Lhuilier |
|
|
|
1813 |
Augustin
Cauchy (1798-1857)
|
|
|
|
1840 |
August
Möbius (1790-1868) Astronome Leipzig |
|
|
|
1852 |
Francis
Guthrie (1831-1899) Mathématicien et botaniste Anglais alors professeur à
la South African University, Cape Town (Afrique du Sud)
|
|
|
|
1852 |
Auguste
De Morgan (1806-1871) University College, Londres
William
Hamilton (1830-1803) Irlandais
|
Le 23 octobre 1852 ; lettre
d'Augustus de Morgan, professeur de mathématiques à University College
(Londres) à Sir William Rowan Hamilton, professeur au Trinity College
(Dublin): "… Si quatre régions ont deux à deux
une ligne frontalière, trois d'entre elles enclavent la quatrième et
empêchent n'importe quelle cinquième de la toucher. Si ceci était vrai,
quatre couleurs seraient toujours suffisantes…" Hamilton répond qu'il n'a guère le temps
(l'envie) de s'intéresser à ce problème de quaternion
de couleurs (I'm not likely to attempt your "quaternion" of colours
very soon).
Extrait de la lettre 23 octobre 1852
Il est impossible de disposer cinq régions
de telle façon qu'il existe des frontières communes entre tous les couples
possibles. Propriété qui laisse penser que quatre
couleurs devraient suffire. |
|
1860 |
De Morgan
William Whewell Philosophe |
(…)
Now, it must have been always known to map-colourers that four different
colours are enough. (En
fait, les cartogrpahes ont toujours su que quatre couleurs sont suffisantes). |
|
1869 |
Charles
Sanders Pierce Américian |
|
|
1973 |
Carl
Hierholzer (1840-1871) |
|
|
1878 |
Arthur
Cayley (1821-1895)
|
C'est la première référence écrite énonçant le problème et sollicitant une
réponse. |
|
1879 |
Alfred
Kempe (1849-1922)
|
|
|
1880 |
Peter
Tait (1831-1901) et Julius
Peterson |
|
|
1885 |
Thomas
Penyngton Kirkman |
|
|
1885 |
Richard
Baltzer Géomètre allemand |
|
|
1886 |
/ |
|
|
1890 1891 |
(1861-1955)
|
|
|
1891 |
Lothar
Heffter |
|
|
1900? |
Heinrich Tietze (1880-1964) |
|
|
1904 |
Paul Wernicke Allemand |
|
|
1913 |
George
D. Birkhoff (1884-1944) Harvard
|
|
|
1922 |
Philip
Franklin (1898-1965) MIT |
1926, Reynolds donne 27; 1940, Winn arrive à 35; 1970, Ore et Stemple à 39; et 1976, Mater atteint 95.
|
|
1940 |
Henri
Lebesque (1875-1941) |
|
|
Hermann
Minkowski (1864-1909) prend ce problème de haut en prétendant que seuls des
mathématiciens de troisième catégorie auraient étudié ce problème. Ce qui
expliquerait qu'il ne soit pas encore résolu. Il entreprend son étude et
reconnait quelque temps plus tard: "J'ai indisposé le ciel par mon
arrogance: ma démonstration est, elle aussi, inexacte". (Heaven is angered by my arrogance;
my proof is also defective). |
|
1950 à 1970 |
Henrich
Heesch (1906-1995) Hanovre Dürre (le
programmeur) Jean
Mayer Montpellier |
|
|
1959 |
HSM
Coxeter Géomètre |
|
|
1968 |
G. Ringel et E. Youngs |
|
|
1970 |
Wolfgang
Haken (né en 1928) |
|
|
1976 |
Kenneth Appel (1932-2013) et Wolfgang Haken
John Coke Programmeur |
|
|
1995 |
Neil
Robertson (né en 1938), Daniel
Sanders, Paul
Seymour (né en 1950) et
Robin Thomas (né en 1962) |
|
|
2004 |
Georges
Gonthier (Cambridge)
et
Benjamin Werner (INRIA-France) |
Voir Preuve concernant l'empilement des sphères |
|
2005 |
J.
Ferro |
Reference 1: The four color
theorem – MathWorld J. Ferro (pers. comm., Nov. 8, 2005) has debunked a number
of purported "short" proofs of the four-color theorem. Traduction: J. Ferro
(communication personnelle du 8 novembre 2005) a démystifié un certain nombre
de prétendues courtes preuves du théorème des quatre couleurs. Reference 2: Vertex
Coloring of Planar Graphs with Restrictions over Shortest Paths. |
|
2014 |
/ |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/TopoQHis.htm
|
![]()