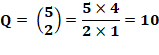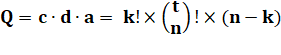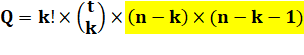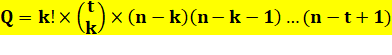|
||||||||||||||||||||||||||||||||||||||||
![]()
|
LOTO traditionnel avec cartons Loto familial Calcul de probabilités Les pages
précédentes présentent le calcul de la quantité de
cartons possibles au loto traditionnel. Cette
page s'applique au calcul de probabilités.
Par exemple, quelle est la probabilité de couvrir une ligne (quine) dès la
cinquième annonce, la sixième, etc. On
commence par une approche simple, puis l'examen de quelques cas pour élaborer
une formule de calcul. Une exploration par ordinateur prendrait beaucoup trop
de temps. En revanche, on utilise l'exploration par ordinateur pour valider
la formule pour de petites valeurs. |
Anglais: Bingo / Bingo Lotto Lottery with
tickets / Tambola ticket
Notations et formule
|
k = [1, 2, 3, 4, 5], n = 1 à 90, 6t => Q = sur T = k = 5 est la quantité de nombres sur la ligne du
carton (désigne aussi les 5 nombres parmi 90). n = 90 est la quantité de boules dans l'urne,
numérotée de 1 à 90. t comme tirages:
indique que t boules seront tirées de l'urne. Q =
quantité de cas où les six tirages donnent k (cas favorables). T = quantité de possibilités pour les six
tirages. P = Q / T = probabilité de gagner.
|
![]()
Approche –
Principe de dénombrement
|
Approche – 1 numéro pour 3
boules |
|
|
|
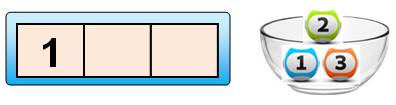
Jeu
Mon
carton: trois cases avec le numéro 1. Les
boules: trois numérotées de 1 à 3. Tirage: 2
fois. Quelle
est ma probabilité de gagner ? Solution
Notation de ce cas k = [1], n = 1 à 3, 2t |
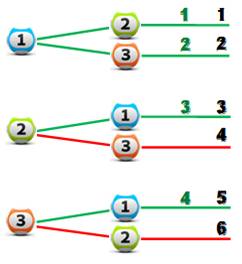
Après deux tirages: 4 cas favorables sur 6 Une autre manière de calculer la probabilité: compter toutes les
possibilités (6) et ne retenir que les cas favorables (4)
Notez que: Il y a 3 cas au premier tirage puis 2 au second. Soit un total de 3 x
2 = 3! = 6, un
nombre à l'allure factorielle. |
|
|
Approche – 2 numéro pour 5
boules |
|
|
|
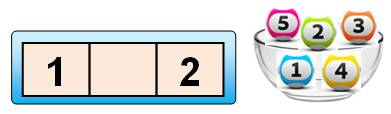
Jeu
Mon
carton: trois cases avec les numéros 1 et 2 (ou tout autre couple). Les
boules: trois numérotées de 1 à 5. Tirage:
2. Quelle
est ma probabilité de gagner ? Solution Premier tirage le 1 avec 1/5 puis 1/4 pour le 2. Premier tirage le 2 avec 1/5 puis 1/4 pour le 2. Soit 2 x 1/5 x 1/4 = 1/10 Notation de ce cas k = [1,2], n = 1 à 5, 2t |
Quantité de possibilités
Soit 5 x 4 = 20 possibilités de tirages. Calcul Après deux tirages dans l'urne on dispose de:
Soit 2 cas gagnants 20 cas possibles. Probabilité de gagner: 1chance sur 10. Notez que: Le résultat est la quantité de combinaisons de 2 parmi 5.
|
|
![]()
Méthode de dénombrement
du plus simple au plus complexe
et aux solutions pour le loto
|
k =[1,2], n = 1 à 4, 3t |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
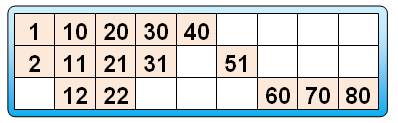
Étape 00 de la méthode Quantité totale de possibilités: T = 4 x 3 x 2 =
24 Étape 0 de la méthode Établir une matrice des possibilités gagnantes. Sur le tableau ci-dessous, chaque ligne
représente le jeu de boules successivement tirées. |
Étape 1 de la méthode (mauve) Compter les possibilités de placer les numéros de mon carton (ici: 1 et 2) dans la matrice
selon leurs permutations ( ici: [1, 2] et [2, 1]) Étape 2 de la méthode (blanc) Compter les emplacements possibles de ces numéros sur une ligne. Étape 3 de la méthode (jaune) Compter les possibilités de rangement des nombres qui ne sont pas sur
mon carton. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Cas simple pour illustrer la méthode Trois boules sont tirées de
l'urne en trois titrages (t1, t2 et t3 les colonnes du tableau).
|
1)
Deux nombres sur le carton avec leurs permutations:
[1, 2] et [2, 1] = > c = 2 2)
Disposition de ces 2 nombres sur chaque ligne: combinaisons
de 2 parmi 3: d = 3
3)
Autres nombres à placer: Gagnants: Q = 2 x 3 x 2 = 12 Formule provisoire (qui va être justifiée plus loin)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Dénombrement
– Panorama
|
k =[1,2], n = 1 à 4, 4t |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Avec quatre tirages et deux
nombres sur mon carton, il reste deux colonnes pour placer les nombres
restants (jaune)
Évidemment, avec quatre boules et quatre tirages on est gagnant à tout
coup ! |
Total: T = 4 x 3 x 2 x 1 = 24 Permutations: c = 2 Disposition des 2 nombres du carton: combinaisons de 2 parmi 4: d = 6
Autres nombres: a = 4 – 2 = 2 Gagnants: Q = 2 x 6 x 2 = 24 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
k =[1,2,3], n = 1 à 5, 4t |
|
|||||||||||||||||||||
|
Total: T = 5 x 4 x 3 x 2 = 120 Permutations: [1, 2, 3], [1, 3, 2], …
= > c = 6 Disposition des 3 nombres du carton: combinaisons de 3 parmi 4: d = 4 Autres nombres: a = 2 Total: Q = 6 x 4 x 2 = 48 |
|||||||||||||||||||||
|
idem avec n de 1 à
10 |
Total: T = 10 x 9 x 8 x 7 = 5 040 Permutations: c = 6 Disposition des 3 nombres du carton: combinaisons de 3 parmi 4: d = 4 Autres nombres: a = 7 Total: Q = 6 x 4 x 7 = 168 soit 1 chance sur 30. |
|||||||||||||||||||||
|
k =[1,2], n = 1 à 10, 4t |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Total: T = 10 x 9 x 8 x 7 = 5 040 Permutations: c = 2 Disposition des 2 nombres du carton: combinaisons de 2 parmi 4: d = 6 Autres nombres: 8 nombres dans deux cases a = 8 x 7 = 56 Total: Q = 2 x 8x7 x 6 = 672 Formule (Révision)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
k =[1,2,3], n = 1 à 15, 5t |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Total: T = 15 x 14 x 13 x 12 x 11 = 360 360 Permutations: c = 3! = 6 Disposition des 3 nombres du carton: combinaisons de 3 parmi 5: d = 10 Autres nombres: 12 nombres dans deux cases c = 12 x 11 = 132 Total: Q = 6 x 12x11 x 10 = 7 920 |
||||||||||||||||||||||||||||||||||||||||||||||
|
k =[1,2,3], n = 1 à 10, 8t |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Total: T = 10x9x8x7x6x5x4x3 = 1 814 400 Permutations: c = 3! = 6 Disposition des 3 nombres du carton: combinaisons de 3 parmi 8: d = 56 Autres nombres: 7 nombres dans 5 cases a = 7x6x5x4x3 = 2 520 Total: Q = 6 x 56 x 2 520 = 846 720 Formule (Finale)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
Cas du Loto
traditionnel avec ses 90 nombres
|
k =[1,2,3,4,5], n = 1 à 90,
5t
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Total: T = 90x89x88x87x86 = 5 273 912 160 Permutations: c = 5! = 120 Aucun autre nombre à distribuer Aucune autre manière de loger les 5 nombres dans une ligne Total: Q = 120 x 1 x 1 = 120 |
||||||||||||||||||||||||||||||||||||||||||||||
|
k =[1,2,3,4,5], n = 1 à 90,
6t
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Total: T = 90x89x88x87x86x85 = 448 282 533 600 Permutations des nombres du carton: c = 5! = 120
Total: Q = 120 x 6 x 85 = 61 200 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple de lecture de
ce tableau avec tous les paramètres de calcul La probabilité de gagner avec une
ligne de nombres sur un carton après 10 tirages est: 1 sur 174 401.
Exemple de lecture de
ce tableau donnant les probabilités pour 5 à 54 tirages La probabilité de gagner une ligne
après 15 tirages est: 1 sur 14 635.
Avec trois lignes
La probabilité de gagner sur chaque
ligne est celle des tableaux. Pour terminer une des trois lignes,
c'est le triple de la probabilité exprimée en Q/T (nombre entre 0 et 1). La probabilité d'un carton plein est
le cube des valeurs de Q/T. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Au
cours de ces pages nous avons vu comment:
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette
page |
![]()