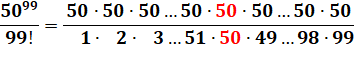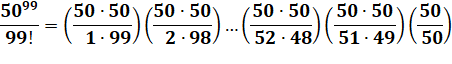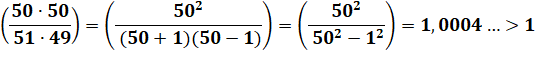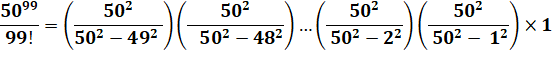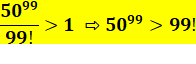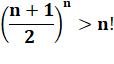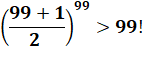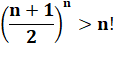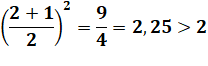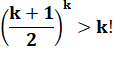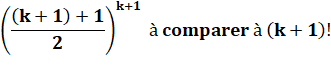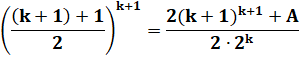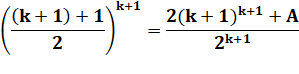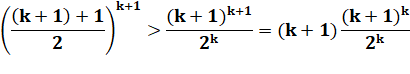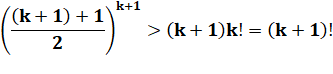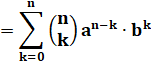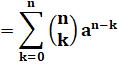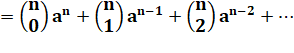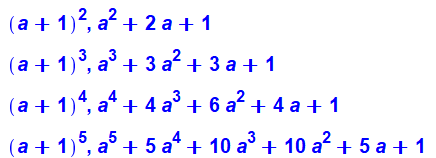|
Édition du: 17/09/2023 |
|
INDEX |
Problèmes – Défis |
||
|
Équations
en x, y, z |
|||
|
Équation en
x4 |
|||
![]()
|
Comparer: 5099 et 99! Comment
manipuler de telle quantités et trouver laquelle des deux est la plus grande. Démonstrations. |
||
|
|
Sommaire de cette page >>> Comparaison entre 5099 et 99! >>> Inégalité – Démonstration par induction >>> Calcul de la puissance du binôme >>> Termes de degré inférieurs – Pour info. |
Débutants Glossaire |
Valeurs numériques pour info.

99! =
37,6231004…99
|
Développement de ces valeurs Il s'agit de montrer que cette fraction est
supérieure à 1. Aa numérateur comme au dénominateur, il y a 99
facteurs et 50 est au centre. |
|
|||||
|
Regroupement Au dénominateur, les nombres après 50 sont
appariés de façon telle que la somme fasse 100. |
|
|||||
|
Remarquons que:
|
|
|||||
|
Nouvelle écriture |
|
|||||
|
Chaque facteur est supérieur à 1 |
|
|||||
|
Vérification Avec 50, le rapport dépasse 1012 Avec 38, le rapport est égal à 2,68… Rapport |
|
|
||||
|
Preuve directe connaissant cette
inégalité |
|
|
||||
|
Démonstration de cette inégalité par induction |
|
|
|
Cas de référence: vrai pour n = 2 |
|
|
|
Hypothèse: on suppose que l'inégalité est vraie
pour k |
|
|
|
Démonstration: |
|
|
|
Développement |
|
|
|
La quantité A est plus grande que 0 On minimise l'expression en la retirant |
|
|
|
Traduction en inégalité et |
|
|
|
Remplacement par l'hypothèse tenue pour vraie |
|
|
|
Conclusion |
Cas référence vrai et si vraie pour k alors vraie pour k+1 implique
que l'inégalité est toujours vraie. |
|
Calcul de la
puissance du binôme
|
|
|
|
|
|
|
|
|
|
|
Exemples
|
|
|
Valeurs intermédiaires selon le triangle de
Pascal |
|
|
|
|
|
|
|
|
|
Voir Développement
d'un binôme à la puissance k / Binôme de Newton
|
Par curiosité, évaluation des termes de degrés
inférieurs avec exemples. Dans le cas du binôme (a + 1) à une puissance, la
somme des deux premiers termes dépasse largement la somme de tous les autres
termes. Le tableau montre des exemples numériques avec
les plus petites valeurs de a. Dit-autrement: malgré la présence de coefficient
binomiaux de plus en plus grands, ils ne compensent pas la croissance des
deux termes de degrés supérieurs. |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aExercic/Probleme/Compar99.htm |