NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/10/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	TOPOLOGIE
Débutants Géométrie	QUATRE COULEURS			Glossaire Géométrie
INDEX Quatre couleurs Topologie	Démonstration en bref	Démo de Kempe	Démo d'Appel et Hanke
		Sommaire de cette page >>> Stratégie de démonstration >>> Cas de deux frontières >>> Cas de trois frontières >>> Cas de quatre frontières >>> Cas de cinq frontières >>> Théorème de Kempe >>> Contre exemple de Heawood >>> Passage à trois arêtes

Théorème des quatre couleurs

Démonstration originale de Kempe

La première démonstration qui s'avéra fausse mais qui:

permettra la démonstration du théorème des cinq couleurs,

donnera toutes les bases pour la démonstration pour quatre couleurs.

Voir Historique

Stratégie de démonstration
Il s'agit d'une démonstration par contradiction.	L'hypothèse est faite qu'il faut cinq couleurs au plus. Un raisonnement conduit au fait que c'est contradictoire. Conclusion: il n'en faut que quatre.
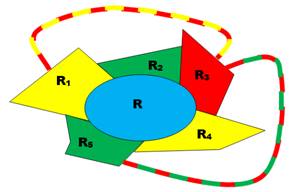
Si le théorème des quatre couleurs et faux, c'est qu'il en faut une cinquième.	Il existerait des cartes qui nécessitent cinq couleurs. Parmi toutes celles-ci, intéressons nous à celles qui sont juste à la limite; celles qui, si on retire une seule région, sont finalement colorables avec quatre couleurs. Ce sont les cartes minimales En fait: des contre-exemples du théorème des quatre couleurs.
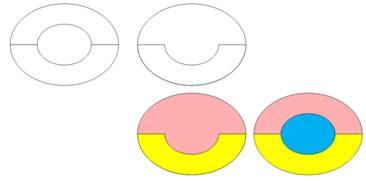
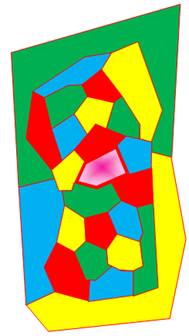
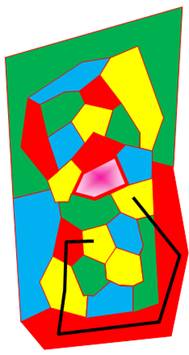
La stratégie consiste à réduire les cartes minimales et monter que le résultat est impossible.	Une région est momentanément réduite en un point. S'agissant d'une carte minimale, lui ôter une région la rend 4-coloriable. L'idée est démontrer qu'en réintégrant la région réduite, la carte reste 4-coloriable. C'est là qu'est la contradiction.
Kempe trouve quatre types de régions à examiner: les régions à 2, 3, 4 ou 5 frontières (arêtes).	Il montre qu'il sait opérer la réduction et produire une carte 4-coloriable Les cas 2, 3 et 4 côtés sont indiscutables. Il pensait avoir résolu le cas à 5 côtés qui va s'avérer finalement très, très complexe.

Cas de deux frontières (digone)

Supposons une carte minimale à cinq couleurs qui possède une région à deux frontières. Zone centrale sur l'illustration. On l'a réduit à un point. La carte minimale perdant une région devient 4-coloriable. La partie concernée est coloriable avec seulement deux couleurs. Et, réintroduire la région centrale réduite peut être colorié avec la troisième ou la quatrième couleur, au choix. Moralité: la carte initiale supposée 5-coloriable est finalement 4-coloriable. Dis-autrement: si une carte 5-coloriable existe, elle ne comporte pas de régions à deux frontières.

Cas de trois frontières (triangles)

Supposons une carte minimale à cinq couleurs qui possède une région à trois frontières (D). Si D est fondue dans C pour devenir C' (ou D réduite à un point), alors la carte résultante a moins de régions qu'une carte minimale à cinq couleurs. Du fait que la carte est minimale, la carte ainsi réduite ne nécessite plus que quatre couleurs. Sur cette nouvelle carte à quatre couleurs, nous devons réintroduire la zone D. Or les trois zones A, B et C' n'utilisent que trois couleurs. Il suffit d'attribuer la quatrième couleur à D. Ainsi, une carte minimale qui comporte un triangle est 4-coloriable et mon par 5. L'hypothèse est fausse.

Cas de quatre frontières (quadrilatères)
Cette fois nous avons quatre régions entourant la région centrale sur l'illustration. Momentanément, nous réduisons la région centrale en un point. La carte minimale à cinq couleurs est réduite à une carte 4-coloriable. Au pire, les quatre couleurs sont nécessaires. Ici, Kempe a mis au point une technique qui sera reprise par tous ses successeurs: la technique des chaines de Kempe En partant de la région rouge, existe-t-il une chaine de rouge/ bleu qui relierait la région bleue? Si tel est le cas, il n'existe pas de chaine jaune/verte qui relierait les deux autres, sinon les deux chaines se croiseraient. Il est possible d'intervertir les couleurs dans la chaine jaune/verte sans "polluer" l'autre chaine. La région jaune devient verte. Reste trois couleurs et la possibilité de réintroduite la zone centrale avec du jaune. Dans le cas où il n'y a pas de chaine formant un circuit, alors l'échange est possible et le cas est résolu.	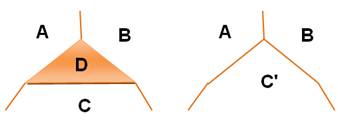On montre, ici encore, qu'une carte hypothétique 5-coloriable minimale ne peut pas comporter une telle région à quatre frontières.

Cas de cinq frontières (pentagone)
Cinq régions entourent la région R. Si les cinq régions sont colorées avec moins de quatre couleurs, la région centrale R prend la quatrième couleur
R1 est la seule région en jaune, R2 est la seule en rouge et ces deux régions ne sont pas connexes. S'il n'existe pas de chaine-circuit jaune/rouge R1R3, on peut intervertir les couleurs dans la ou les chaines jaunes/rouges aboutissant à R1. R1 passe au rouge et le jaune devient disponible pour R.
S'il y a une chaine-circuit R1R3, Nous nous intéressons à R5, seule région verte et aux chaines rouges/vertes au départ de R5. Aucune chaine R3R5. Couleurs interverties. R5 devient rouge et R prend la couleur verte.
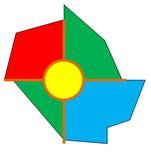
Les deux chaines existent. R1R4 et R2R5 ne peuvent exister sous peine de croiser un circuit existant. On échange les couleurs sur les chaines en R4 et R4 devient jaune. On échange les couleurs sur les chaines en R2 et R2 devient vert. La région centrale R devient bleue. Bilan Dans tous les cas (du moins le pensait Kempe), une carte 5-coloriable minimale ne peut contenir une région ayant cinq frontières.

Théorème de Kempe
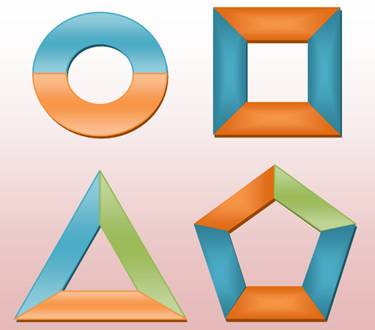
Théorème Dans toute carte, il existe au moins une région avec cinq voisines ou moins. La région est en forme de cercle (2), de triangle (3), de carré (4) ou de pentagone (5). Pour la résolution du problème des quatre couleurs, ces cas sont des cas inévitables.

Conclusion de Kempe

Toute carte, fut-elle 5-coloriable, contient au moins une région ayant cinq frontières ou moins. Un de ces cas est inévitable.

Or une hypothétique carte 5-coloriable ne contient aucune des cinq configurations.

Cette carte hypothétique n'existe pas.

Le contre-exemple de Heawood
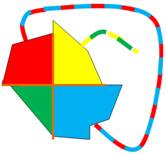
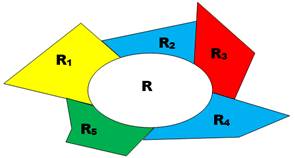
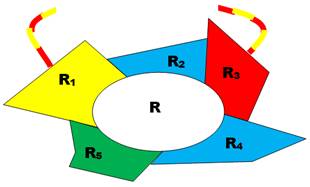
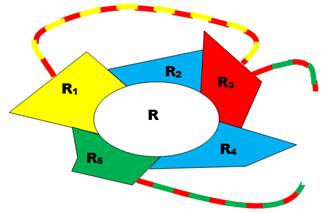
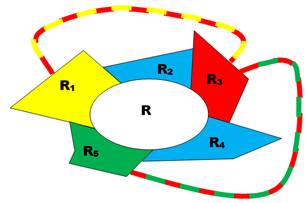
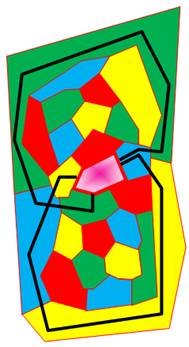
C'est Heawood qui, quelques années plus tard, montra que la preuve de Kempe était incomplète. Il mit en évidence ce contre-exemple (Ci-contre). Il applique la méthode des chaines de Kempe: En haut à droite, identification de deux chaines-circuits qui entraînent l'inversion des couleurs sur deux autres chaines interrompues. Il obtient bien trois couleurs autour de la zone centrale, mais en prime deux zones rouges qui se côtoient. Heawood parviendra néanmoins, sur la base des travaux de Kempe, à démontrer le théorème des cinq couleurs. Il en profite aussi pour étudier la coloration des volumes.

Simplification

Sans encore avoir découvert l'erreur de Kempe, Peter Gunthrie Tait tente de simplifier la démonstration. Elle toute aussi erronée, mais il introduit la triangulation des cartes qui va servir par la suite. Si la nouvelle carte est 4-coloriable, alors l'originale l'est aussi.

Gunthrie appuyait sa démonstration sur un lemme admis disant qu'une carte triangulée est 3-coloriable. ce qui est vrai. Mais, il n'avait pas conscience que ce lemme est équivalent au théorème des quatre couleurs et donc aussi difficile à prouver.

Retour Suite	Démonstration en bref Démo d'Appel et Hanke (déjà vu si vous suivez ce fil) Historique Quatre couleurs – Index
Voir	Cinq pays Couleurs Démonstration Énigme des carrés mitoyens Graphe à 2 couleurs Indicateur d'Euler-Poincaré Introduction à la topologie Passage à trois arêtes (triangulation) Quadrichromie Topologie - Glossaire Topologie – Index
DicoNombre	Nombre 4
Sites	Voir références
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/DemoKemp.htm