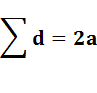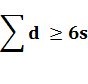|
|||||||||||||||||||||||||||||||||||
![]()
|
Théorèmes des quatre couleurs Relation d'Euler La relation d'Euler bien
connue pour les polyèdres,
s'applique aussi aux graphes. C'est elle qui permet de faire de
l'arithmétique avec le degré des sommets et, à partir de certaines
inégalités, en déduire des propriétés de coloration des graphes. |
|
|
|||||||||||||||||||||||||||||||||
|
La relation d'Euler
s'écrit: s
– a + f = 2 sommets –
arêtes + faces = 2 y compris face
externe. La quantité 2 est la caractéristique d'Euler pour les
graphes (et les polyèdres convexes); elle peut être différente pour d'autres
objets (0 pour le tore par exemple). Illustration et principe de réduction (qui donne une idée
de la démonstration de cette relation)
Ne pas oublier de compter la face externe au graphe Degré d'un sommet Le degré d'un sommet est égal à la quantité d'arêtes
issues de ce sommet. Une boucle sur un sommet compte bien sûr pour 2. Comme chaque arête connecte deux sommets, la somme des
degrés d'un graphe est égale au double de la quantité d'arêtes.
Autre propriété: K Le nombre chromatique d'un graphe est toujours inférieur ou égal au degré maximum trouvé dans le graphe plus 1. Relation d'inégalité En utilisant la relation d'Euler, on établit l'inégalité: a
Laquelle va servir à montrer des incompatibilités et
ainsi progresser dans la démonstration du théorème des quatre couleurs (ci-dessous). |
|||||||||||||||||||||||||||||||||
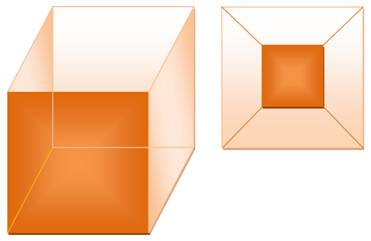
Voir Formule d'Euler et
polyèdres
|
|
||
|
Supposons un graphe dont tous les sommets ont un degré
égal à 6 ou plus. |
Somme des degrés supérieure ou égale à six fois la quantité des
sommets. |
|
|
Avec cette quantité de sommets, il y au moins la moitié
de sommets |
s
|
|
|
Pour ce graphe comme pour tout graphe |
a
|
|
|
Contradiction! |
Il existe au moins un sommet de degré inférieur à 6. |
|
|
L'idée consiste alors à réduire le graphe à partir de
ce sommet (ou l'un de ces sommets) et le colorier en faisant marche arrière. |
Alors, reprendre le graphe dans l'ordre inverse. Colorer le sommet à
chaque fois en terminant par le sommet choisi de degré inférieur à 6. Les couleurs sont hiérarchisées et la couleur choisie pour un sommet
et la première encore disponible. |
|
|
Le choix est toujours possible parmi les six couleurs. |
Durant la progression de la mise en couleur, il y a au plus cinq
sommets voisins qui ont été colorés. La sixième couleur est toujours
disponible. |
|
|
Conclusion: six couleurs suffisent à colorier tout graphe planaire. |
||
|
La
preuve pour cinq couleurs est du même type. Tombant
sur l'obligation d'utiliser la sixième couleur, un retour arrière permet de
trouver un autre chemin qui ne mobilise que cinq couleurs. La
preuve pour quatre couleurs est plus ardue. Elle consiste
à montrer qu'un graphe nécessitant plus de quatre couleurs conduit à une
contradiction. Elle passe par le fait que subsiste une quantité finie de
configurations inévitables. |
|
|
||
|
|
|
|
|
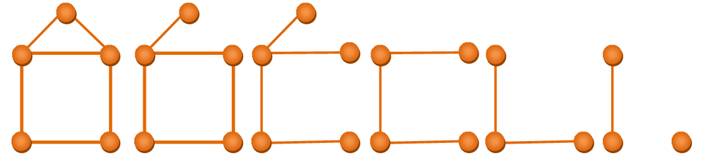
S = 8 F = 10 + 1 externe A = 17 S – A + F = 8 – 17 + 11 = 2 La relation d'Euler est
vérifiée |
|
|
|
S = 8 F = 9 + 1 externe A = 16 S – A + F = 8 – 16 + 10 = 2 |
|
|
|
Cette démonstration est similaire à celle montrée pour les graphes. Ici, elle est démontrée pour les polygones. |
||
![]()
|
Retour Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/CouEuler.htm
|
![]()