NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 23/09/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ÉLÉMENTS de base
Débutants Géométrie	Généralités			Glossaire Géométrie
INDEX Géométrie Constructions	Bases	Point	Droite	Plan
		Parallèle	Perpendiculaire	Orthogonal
		Égalité	Distance	Angle
		Sommaire de cette page >>> Perpendiculaire >>> Types >>> Construction >>> Perpendiculaire avec la règle uniquement

Perpendiculaires

Droites orthogonales

Définition et propriétés.

Attention, nous sommes en géométrie plane.

Perpendiculaire
Droites qui forment un angle droit (90°) entre-elles. On note: () (') Remarque: dans le plan les droites, sauf à être parallèles, se coupent toujours. D'où l'emploi de l'adjectif perpendiculaire et non orthogonal. Voir Subtilité de vocabulaire concernant l'orthogonalité Axiome Soit une droite () et un point M quelconque du plan. Par le point M il passe une droite et une seule perpendiculaire à (). Théorèmes Si deux droites sont perpendiculaires à une même troisième droite, alors elles sont parallèles entre elles. () (1) et () (2) => () // (2) Si deux droites sont parallèles, alors une perpendiculaire à l'une est aussi perpendiculaire à l'autre. () // (2) et () (1) => () (2)

Types de perpendiculaires
Normale	Droite normale à un plan: droite qui est perpendiculaire à deux droites distinctes de ce plan.
Verticale	Droite perpendiculaire au plan horizontal ou perpendiculaire à deux droites horizontales distinctes. Souvent assimilée à l'axe des y dans un repère à deux axes ou des z dans un repère a trois axes.
Hauteur	Dans un triangle, perpendiculaire à un côté, issue du sommet opposé.	>>>
Apothème	Sorte de hauteur - polygones réguliers: droite issue du centre et perpendiculaire à un côté. - pyramides régulières: droite issue du sommet et perpendiculaire à un côté.
Médiatrice	Perpendiculaire à un segment en son milieu.	>>>
Hypoténuse	Dans un triangle rectangle, côté opposé à l'angle droit.
Repère	Ou système d'axes orthogonaux.	>>>

Construction à partir d'un point sur une droite
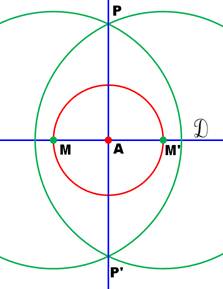
Méthode du triangle isocèle Construire la perpendiculaire en A à la droite D. 1. Cercle de centre A de rayon quelconque. Il coupe la droite en M et M'. 2. Cercles de centre M et M' de même rayon quelconque. Ils se coupent en P et P'. 3. La droite PP' est la perpendiculaire recherchée. Note: PP' est la médiatrice de MM'
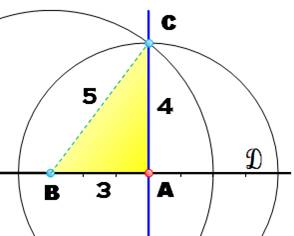
Méthode de l'architecte, de l'arpenteur, du maçon ou du jardinier ou encore méthode 3-4-5 Construire la perpendiculaire en A à la droite D. 1. Placer B à trois unités de A sur la droite D. 2. Cercle de centre A avec 4 unités de rayon. 3. Cercle de centre B avec 5 unités de rayon. On reconnait le célèbre triangle rectangle 3-4-5 d'où le nom de la construction. Voir Méthode du jardinier et le théorème de Pythagore
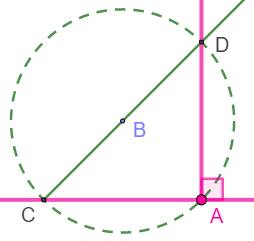
Méthode express Construire la perpendiculaire en A à la droite. 1. Point B quelconque 2. Cercle (B, BA). Intersection C. 3. Demi-droite CB. Intersection D. 4. Demi-droite AD perpendiculaire en A à AC. Justification CD est un diamètre. L'angle CAD intercepte un diamètre, il est droit.

Voir Constructions élémentaires

Construction à partir d'un point hors de la droite
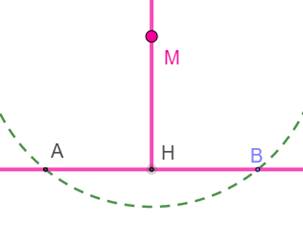
Construire la perpendiculaire à la droite horizontale passant par le point M. 1. Cercle de centre m et de rayon quelconque coupant la droite. Intersections A et B. 2. Milieu H de AB 3. la demi-droite HM est perpendiculaire à la droite AB. MH est la hauteur, médiane, médiatrice et bissectrice du triangle isocèle AMB.

Perpendiculaire avec la règle uniquement			haut
Théorème	Toute construction à la règle et au compas peut être réalisée avec la règle seulement, à condition de diposer d'un cercle.
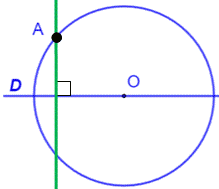
Problème Un point A sur un cercle. Une droite D passant par le centre du cercle. Comment tracer la perpendiculaire en A à D à la règle, sans compas ? Pistes 1) Former un triangle et ses trois hauteurs Profiter du diamètre du cercle pour tracer deux angles droits, lesquels porteront les perpendiculaires d'un triangle. En profiter pour dessiner la troisième perpendiculaire qui sera naturellement perpendiculaire à la droite D et donc parallèle à la droite cherchée. 2) Translater la perpendiculaire trouvée pour l'amener au point A.		Pour tracer la perpendiculaire à D en A: former l'orthocentre d'un triangle, puis utiliser la médiatrice pour trouver le symétrique de A par rapport à D.
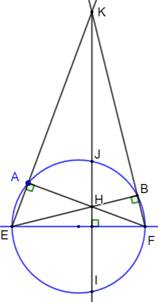
Construction du triangle et ses hauteurs Prendre un point (B) quelconque sur le cercle. Tracer les demi-droites EA et FB qui se coupent en K. Tracer les segments EB et FA qui se coupent en H, l'orthocentre du triangle EFK. En effet les angles AEF et EBF, interceptant un diamètre, sont droits. 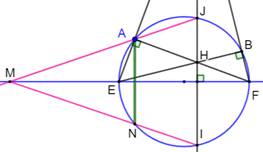Conséquence: La droite KH porte la troisième hauteur du triangle et, perpendiculaire à EF, elle est parallèle à la perpendiculaire cherchée. Comment construire la parallèle en A à KH ? Construction de la perpendiculaire cherchée La droite KH coupe le cercle en I et J, deux points symétriques par rapport à la droite EF. La droite JA coupe la droite EF en M. La droite IM coupe le cercle en N. La droite verte AN est perpendiculaire à la droite EF. C'est la droite cherchée.

Suite	Cercles orthogonaux Parallèle Orthogonalité Égalité Éléments de bases de la géométrie
Voir	Bases de la géométrie Cinquième postulat Constructions avec des allumettes Euclide Euclide et contemporains Géométrie - Glossaire Géométrie - Index Jeux Les Éléments Les trois géométries Polygones Symétries motifs de frises et tapisseries
Site	A beautiful and challenging geometry construction – Mind Your Decision – Preh Talwarker Geometrical constructions using only a ruler – Njteh Mkhsian and Lory Aintablian
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Perpendi.htm