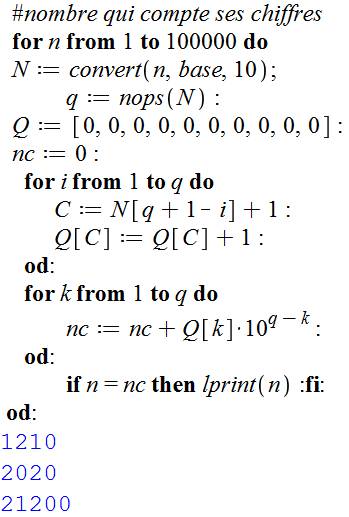|
Édition du: 16/12/2024 |
|
INDEX |
CHIFFRES – Fréquence |
||
Faites
un double-clic pour un retour en haut de
page
![]()
|
Nombres auto-descriptifs Self-descriptive numbers Autobiographical numbers Nombres dont les chiffres indiquent la quantité
de chiffres Ce nombre
(1210) contient un 0, deux 1, un 2 et zéro 3. |
||
|
|
Sommaire de cette page >>> Nombres auto-descriptifs >>> Changement de base >>> Programmation |
Débutants Glossaire |
|
|
|||
|
Ils sont
sept en base 10: En
ajoutant des 0 à droite, on peut prolonger avec 72 100 001 000 821 000 001 000 etc. |
Ces nombres ont des
chiffres qui comptent le nombre de fois que le chiffre apparait. Dans le cas
du dernier nombre, on compte six fois le
0, deux fois le 1, une fois le 2, une fois le 6 et zéro fois les autres. |
||
|
Propriété |
La somme
des chiffres d'un nombre à k chiffres est égale à k. Propriété
qui facilite la recherche. Il suffit d'examiner les partitions décroissantes
de k ayant k chiffres. |
||
|
Structure |
Astucieusement,
le compte commence par les 0. Ce qui permet de placer un grand chiffre en
tête, et de distribuer autant de 0 que nécessaire plus loin. En
commençant par compter les 1, il serait impossible de créer un nombre auto-descriptif.
Si par exemple, un nombre 2 est placé sous le
3, il faudra placer deux 3 qui, à leur tour,
vont exiger trois fois les nombres indiqués; etc. |
||
|
Contexte |
Ce genre
de nombres a été présenté dans la revue "Pour la Science"
d'avril/juin 2008 sous le titre "Jeux de suites" par Éric Angelini. Il est
clairement décrit dans l'encyclopédie des suites de nombres en OEIS
138 480. |
||
|
Anglais |
Self-Descriptive Number: a 10-digit number satisfying
the following property. Number the digits 0 to 9, and let digit n be the
number of ns in the number. There is exactly one such number: 6 210 001
000. From WolframMathWorld |
||
|
|
||
|
Si les
nombres précédents sont considérés
écrits dans la base correspondante à leur longueur, alors on peut les
convertir en base décimale. De sorte que, par exemple, 1210
en base 4 donne 100 en décimal: 1x43 + 2x42 +1x4 + 0 = 64 + 32 + 4 = 100. Notez que pour tous ces nombres la base est égale à la somme des
chiffres: 1 + 2 + 1 = 4. Le dernier chiffre est toujours un zéro. Les nombres en base 10 sont divisible par la base. Ce sont des nombres de
Harshad dans leur base respective |
|
|
|
|
||
|
|
Boucle de recherche pour tous les nombres n de 1
à cent mille. Par la conversion en base 10, N contient la liste
de tous les nombres de n, mais à l'envers. q est la quantité de chiffres dans n. Q est la liste en préparation pour recevoir la
quantité de tel ou tel chiffre dans n. Boucle d'analyse des chiffres de n. Dans C est
placé le chiffre en cours d'analyse, en prenant la liste N à l'envers. Si C = 5, par exemple, le nombre en position 5
dans Q est incrémenté de 1. Cette boucle avec k calcule la valeur (nc) du
nombre formé par la quantité de tel ou tel chiffre. Si ce nombre est égal au nombre initial, demande
d'impression. En bleu, les valeurs trouvées jusqu'à 100 000. Il
suffit de mettre 10 milliards dans la boucle initiale et attendre patiemment
pour obtenir les sept nombres auto-descriptifs. |
|
Voir Programmation – Index
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()