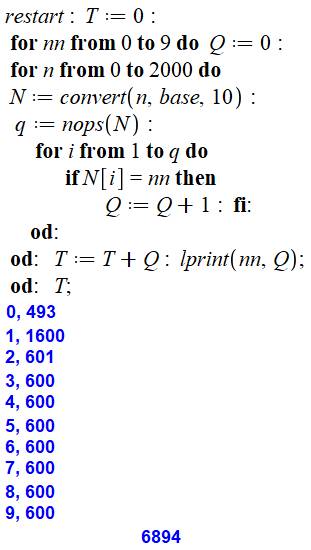|
Édition du: 26/12/2024 |
|
INDEX |
CHIFFRES – Fréquence |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Compter la présence d'un chiffre dans les nombres jusqu'à N Combien doit-on
prévoir de chiffre "1" (ou tout autre non nul) pour écrire tous les
nombres de 0 à N ? Par exemple, on trouve 900
millions de "1" dans tous les nombres de 0 à un milliard (109).
|
||
|
|
Sommaire de cette page >>> Compter les chiffres dans les nombres >>> Cas d'un chiffre donné (non nul) >>> Décompte jusqu'à un nombre n donné |
Débutants Glossaire |
|
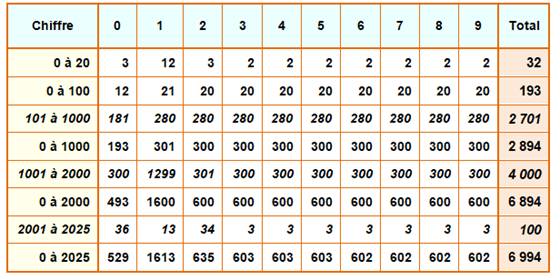
Table Quantité de chiffres pour énumérer les nombres de N à M. Voir Nombre 2025 |
|
||
|
|
Programme Maple But: compter le
nombre de chiffres entre 0 et 2000 (exemple) Commentaires La première boucle fait défiler les chiffres de 0
à 9. La deuxième analyse les nombres de 0 à 2000. Chaque nombre n est converti en suite de chiffres
avec l'instruction convert. La quantité de chiffre dans n est donnée par q. La boucle en i parcoure les chiffres de n, et si l'un
d'entre eux vaut la consigne nn, le compteur Q est incrémenté. A la fin du comptage pour un nombre donné n, le
compte de chiffres Q ets ajouté ua totalisateur T. Bilan En bleu, le résultat du traitement. Entre 0 et
2000 (compris), il y a 493 fois le chiffre"0"; 1600 fois le
"1", etc. Au total, il a 6 894 chiffres pour énumérer tous
les nombres de 0 à 2000. |
||
Voir Programmation – Index
|
De 0 à 9 Le décompte est
immédiat. Prenons l'exemple du chiffre "1":
De 10 à 99 Ce décompte est
simple si on considère séparément les
unités et les dizaines:
De 100 à 999 Même type de
décompte:
De 1000 à 9999 Même type de
décompte:
|
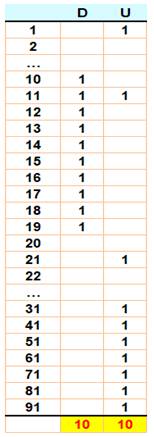
Quantité de 1 dans les nombres de 0
à 99
|
||
|
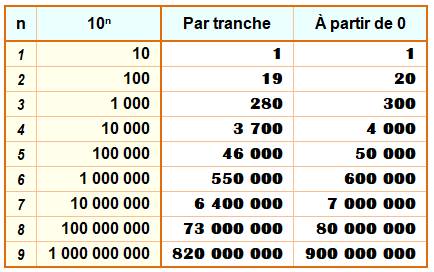
Tableau Ce tableau reprend les décomptes vus ci-dessus et
les prolonge. On donne également la quantité à partir de 0 pour atteindre la
puissance de 10 indiquée (hors cette puissance de 10). Exemple (dernière ligne) On trouve 900 millions de "1" dans tous
les nombres de 0 à un milliard moins 1
(109 – 1). Le 1 de un milliard n'est pas compté. |
|
||
|
Formule Quantité de chiffres "k" non nul de 0 à
10n. Lé décompte réalisé est effectivement valable
quelque soit le chiffre: 1, 2, 3 … hormis le "0". |
|
||
|
Cas du chiffre"0" On trouvera par tranche de puissances de 10: Exemple 180 fois le "0" de 100 à 999. |
0, 9, 180, 2700, 36000, 450000, 5400000, 63000000, 720000000,
8100000000, 90000000000, 990000000000, 10800000000000, 117000000000000,
1260000000000000, 13500000000000000, 144000000000000000, 1530000000000000000,
16200000000000000000, … |
||
|
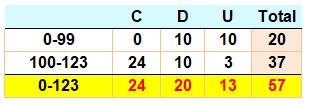
De 0 à 123 avec exemple du chiffre
"1"
|
Quantité de "1" dans les
nombres de 0 à 123
|
|
|
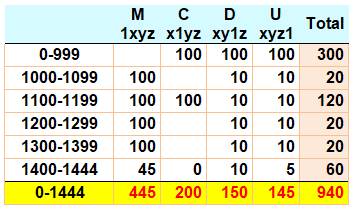
De 0 à 1444 avec exemple du chiffre
"1"
40 fois le 1 en position xy1z, et
|
Quantité de "1" dans les
nombres de 0 à 1444
|
|
Haut de page (ou
double-clic)
![]()
|
Retour |
||
|
Suite |
||
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
||