|
Édition du: 06/05/2023 |
|
INDEX |
CHIFFRES – Fréquence |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Compter la présence d'un nombre dans les nombres jusqu'à N Combien de fois
le nombre 14 (ou tout autre à deux chiffres non nuls) se retrouve dans tous
les nombres de 0 à N ? Par exemple, le
nombre 14 est présent 300 fois dans les nombres de 1 à 10 000; il l'est 900
millions de fois dans les nombres
jusqu'à un milliard. Il est recommandé de commencer à lire la
page sur la présence d'un chiffre dans un
nombre >>> |
||
|
|
Sommaire de cette page >>> Cas du nombre 14 (ou autre sans zéro) >>> Décompte jusqu'à un nombre n donné >>> Exemple complexe avec dix chiffres |
Débutants Glossaire |
|
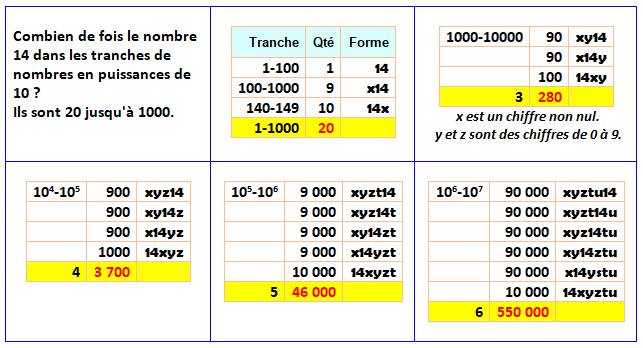
But Dénombrer les nombres 14 présents dans les nombres
de 1 à N, comme dans 14, 145, 514. Dans le cas, par exemple de 1414, le
nombre 14 est compté pour deux occurrences. Le nombre 14 est un exemple. Le calcul s'applique
à tout couple de chiffres sans présence de "0" et sans redoublement
du chiffre. Dénombrement Les premiers nombres avec la présence de 14 sont:
14, 114, 214, ..., 914, soit vingt fois jusqu'à 1000. Le tableau montre le dénombrement par tranches en
puissances de 10.
Le calcul est facilité en considérant la place du
nombre 14 dans les nombres testé. On note la forme de ces nombres: 14xy, x14y
ou xy14, par exemple pour les nombres à quatre chiffres. Alors ces variables x, y ou z prennent toutes les
valeurs de 0 à 9, sauf pour le chiffre en-tête (x) qui ne peut pas être
"0". Notez la forme
sympathique des cumuls: de 0 à 100 000, il y a 20 + 280 + 3 700 = 4 000 fois le 14.
Voir le tableau. Formule pour une tranche en puissance
de 10
Pour la tranche 104 à 105,
où n = 4, on calcule la quantité de 14 jusqu'à 100 000:
|
|
|
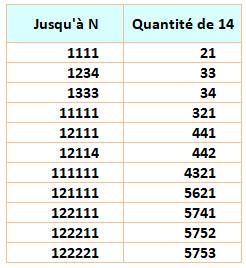
Combien de 14 jusqu'à 1111 Nous savons que jusqu'à 1000, ils sont 20. De 1000 à 1100, une plage de 100, il y en a un
seul. Total: 21 Combien de 14 jusqu'à 1234 Jusqu'à 1000, ils sont 20. De 1000 à 1200, deux plages de 100, il y en a 2. De 1200 à 1234, il y en a un (1214). Sans oublier les nombres en 14x qui sont 10. Total: 20 + 2 + 1 + 10 = 33 |
|
|
|
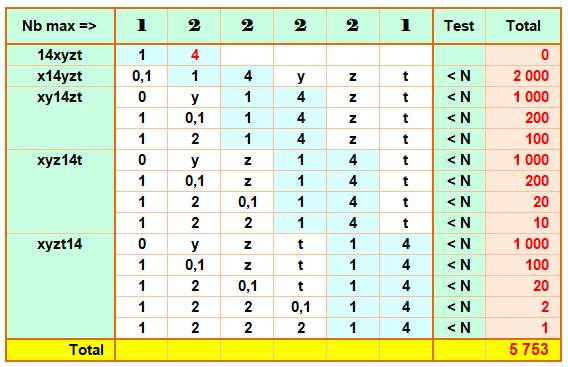
Explication de la dernière ligne:
combien de "14 "jusqu'à 122 221 Le tableau indique: 5 753.
La première ligne rappelle le nombre limite à six
chiffres: 122 221. La première colonne indique la forme des nombres
selon la position du 14. Chaque ligne montre les possibilités de choix des
chiffres. Lorsque la lettre subsiste, alors elle peut prendre toutes les
valeurs de 0 à 9. Par exemple, en deuxième ligne: x14yzt: le
premier chiffre (x) ne peut être que 0 ou 1; puis, derrière le 14, toutes les
valeurs sont permises pour y, z et t: soit 2 × 10 × 10 × 10 = 2000 possibilités. |
||
|
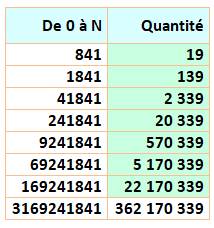
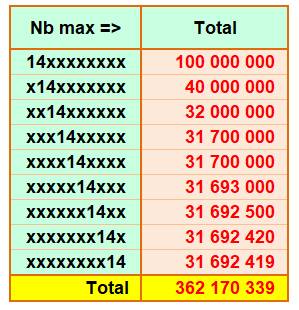
Combien de 14 jusqu'à 3 169 241 841 Le même calcul selon la position du 14 dans les
nombres conduit au tableau ci-contre. Le nombre 14 apparait 362 170 339 fois dans tous
les nombres de 0 à 3 169 241 841. Ces résultats ont été calculés par la méthode vue
ci-dessus et confirmés par programmation de cette méthode. Le dénombrement par exploration systématique des
nombres a été réalisé jusqu'aux neuf derniers chiffres de ce nombre (en
vert).
|
Première ligne: chacun
des huit x prend les valeurs de 0 à 9, soit 108 possibilités. Deuxième ligne: le
premier x est limité à {0, 1, 2, 3}. Le 3 est permis car 314 est inférieur à
316. Les sept autres x peuvent varier de 0 à 9; soit 4 107 possibilités. Etc. |
|
|
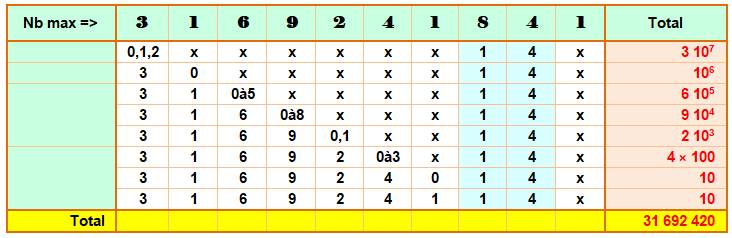
Exemple de calcul pour la
configuration xxxxxxx14x
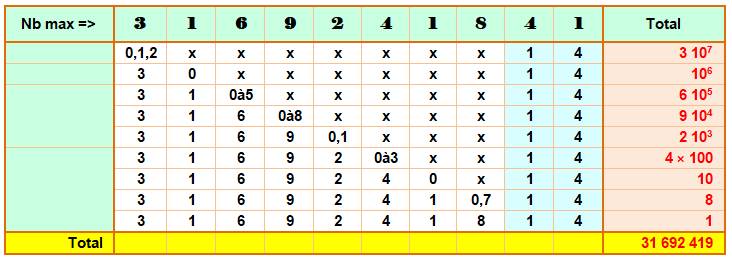
Exemple de calcul pour la
configuration xxxxxxx14x
|
||
Sur une idée de YAN 1954 que je
remercie
Haut de page (ou
double-clic)
![]()
|
Retour |
||
|
Suite |
||
|
Voir |
|
|
|
Cette page |
||