|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Produit de DEUX nombres consécutifs Toujours
divisible par 2 au moins
|
|
|
||
|
Le produit de trois nombres consécutifs est divisible par 2 Que se p |
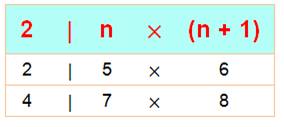
2
| n (n+ 1) Exemple 3 x 4 = 12 = 2 x 6 4 x 5 = 10
= 2 x 5 |
|
|
Note n (n+ 1) = n2
– n Not |
||
|
Note: l |
||
|
|
||
|
Le tableau donne la valeur du
produit Ce produit est divisé successivement
par 2, 4, 8, 16 et 32. En rouge les valeurs non
fractionnaires. |
|
|
|
Conclusions liées aux observations |
n (n+1)
|
|
|
Note: Le c 31 x 32 et 32 x 33 sont divisibles
ch |
||
|
|
||
|
Rempl Cette expression est divisible p Or le produit est déjà divisible par
2 |
n (n + 1) = 4k (4k + 1) = 16k2
+ 4k 4 | n (n + 1) 2 | n (n + 1) |
|
|
Le diviseur 4 l'emporte |
4 | n (n + 1) pour n = 4k |
|
|
L Avec le même r |
n (n + 1) = (4k – 1) 4k = 16k2
- 4k 4 | n (n + 1) pour n = 4k – 1 |
|
|
PPCM:
Plus petit commun multiple. Ici: 4 = 2 x 2 et 6 = 2 x 3 L'un des facteurs 2 est en commun, il ne compte qu'une
seule fois. Les autres sont uniques, ils comptent pleinement. Soit le PPCM de (4 et 6) = 2 x 2 x 3 = 12 |
||
Suite en Divisibilité
du produit de trois nombres consécutifs /
pairs
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/CONSECUT/C2.htm
|
![]()