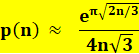NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 28/10/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Théorie des Nombres
Débutants Nombres	COURS			Glossaire Nombres
INDEX Sommaire Partitions	Accueil	Partition (1/2)	Partition (2/2)	Pair et Impair
	Partition PG		Partition en couleurs
	Terminale	Sur la page précédente >>> Orientation >>> Approche >>> Au début: de 1 à 5 >>> Construction pour 6 Sommaire de cette page >>> Application au 7 >>> Table de à 15 >>> Propriétés

PARTITION des NOMBRES

Suite: après avoir vu les partitions des nombres jusqu'à 6, nous poursuivons avec le 7 et donnons le bilan pour tous les nombres jusqu'à 15.

Ramanujan

Sept lentilles. De combien de façons peut-on diviser sept lentilles? Eh bien – il les essaie toutes – on peut les diviser en sept groupes de 1 chacun, ou en un groupe de 6 et un de 1 … Quinze en tout. Oui, on peut diviser sept lentilles de quinze façons. (page 408)

Calculer p(n), le nombre partitions d'un nombre, se révèle facile quand n est un 5 ou un 7 (…) p(n) augmente à un rythme étourdissant (…)le nombre de partitions de 176 est 476 715 857 290. (page 410)

Source: Le comptable indien – David Leavitt

Devinette avec la partition de 13

Devine l'âge de mes trois fils. Je te donne des indices jusqu'à ce que tu sois capable de deviner. OK!

1) La somme de leurs âges est 13.

2) Le produit est égal à votre âge.

3) Mon fils aîné pèse 50 kg.

Stop! C'est bon j'ai trouvé! Et vous?

Réponse

Application au nombre 7

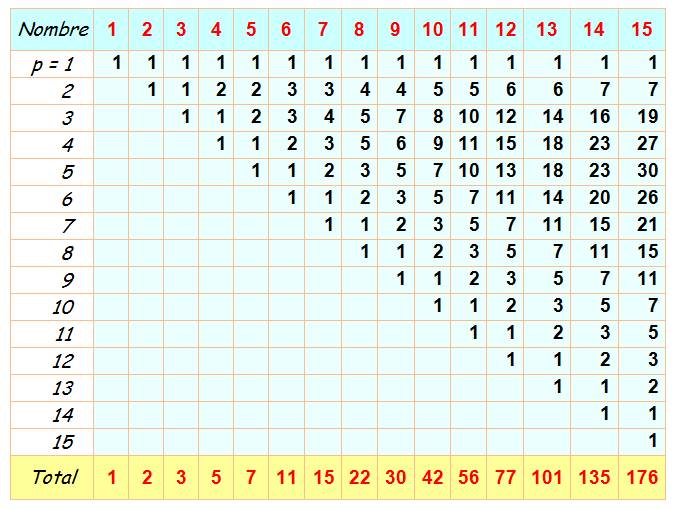
Quantité de partitions

1 - Reprenons le tableau précédent complété des valeurs pour le 6.

2 - Marquons la diagonale partant du 7 (triangle en jaune).

	1	2	3	4	5	6	7
1	1	1	1	1	1	1	1
2		1	1	2	2	3
3			1	1	2	3
4				1	1	2
5					1	1
6						1

3 – Calculons la somme des "jaunes" en la notant en pied de colonne.

4 – Reportons ces valeurs dans la colonne du 7, dans le bon ordre.

5 – Ajoutons la valeur 1 en 7/7 pour comptabiliser la partition du 7 par le 7.

Soit le calcul de la quantité des partitions du 7

	1	2	3	4	5	6	7
1	1	1	1	1	1	1	1
2		1	1	2	2	3	3
3			1	1	2	3	4
4				1	1	2	3
5					1	1	2
6						1	1
7							1
Quantité de partitions	1	2	3	4	3	1	15

La même procédure s'applique pour la construction des colonnes suivantes pour 8, 9, etc.

Calcul de la quantité des partitions du 8

	1	2	3	4	5	6	7	8
1	1	1	1	1	1	1	1	1
2		1	1	2	2	3	3	4
3			1	1	2	3	4	5
4				1	1	2	3	5
5					1	1	2	3
6						1	1	2
7							1	1
8								1
Quantité de partitions	1	2	3	5	5	4	1	22

Cette construction est assez simple en utilisant un tableur.

Table des partitions des nombres de 1 à 15

Voir Formule de récurrence pour établir ce tableau Suite de la table >>> Exemple de lecture de la table: Le nombre 7 peut être vu comme: 15 partitions différentes, ou 14 partitions propres, en retirant la partition de 15 par 15 lui-même. Ces partitions comportent: Une partition avec des 1 uniquement Trois partitions avec au moins un 2 et des 1 Quatre partitions avec au moins un 3 et des poids inférieurs Trois partitions avec au moins un 4 et des poids inférieurs etc. Note: En admettant que 1 + 1 est différent de 1 + 1, alors la quantité de partitions de n de toutes les façons possibles est donnée par une formule simple: 2 ^n - 1 Il existe aussi une formule qui donne une valeur approchée de la quantité des partitions propres.

Voir Tables – Index

Devinette avec la partition de 13

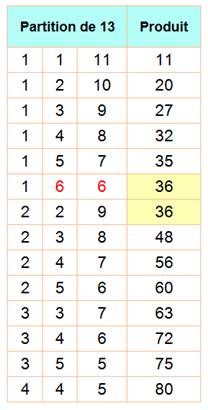
Devine l'âge de mes trois fils. Je te donne des indices jusqu'à ce que tu sois capable de deviner. OK!

1) La somme de leur âge est 13. Il y a 14 possibilités.

2) Le produit est égal à votre âge. Si le copain ne l'arrête pas, c'est qu'il y a indétermination. Le seul tel cas est le produit 36.

3) Mon fils aîné pèse 50 kg. Cet indice indique qu'il y a un aîné. La solution est donc: 9, 2, 2 ans.

Retour

Propriétés

Ramanujan a montré que pour la quantité des partitions:

à partir de n = 5 et tous les 5, la quantité est un nombre divisible par 5 (rouge);

à partir de n = 7 et tous les 7, la quantité est un nombre divisible par 7 (bleus);

à partir de n = 11 et tous les 11, la quantité est un nombre divisible par 11 (verts).

1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490/490, 627, 792, 1002, 1255, 1575, 1958, 2436 …

Il a aussi montré que la quantité de partition est approximativement:

Ex: Pour n = 100 => 199 280 895 pour 190 569 292 (4,5 %)

Pour n = 1000 => 2,44 10³¹ pour 24 061 467 864 032 622 473 692 149 727 991 (1,41 %)

Pour n = 10 000 => 3,63 10¹⁰⁶ pour 3616725 1325636293 9888204718 9095369549 5016030339 3156504220 8186860588 7952568754 0664205923 1055605290 6916435144 (0,44%)

Voir Quantité de partitions

Retour Suite	Partition (début) Partition et polynômes générateurs
En savoir plus	Addition – Glossaire Conjecture de Goldbach Escalier et partitions Nombre d'Ulam Nombres quatrops Pair et impair Partition des nombres de 1 à 10 Partitions – Développements Partitions – Fonctions génératrices Somme des nombres impairs
Références	DicoMot DicoNombre Glossaire mathématique
Voir	Calcul – Index Conjecture de Goldbach Jeux et puzzles – Index Nombres modulo Nombres par leur petit nom Systématique – Index Théorie des Nombres – Index
Site	OEIS A000041 - a(n) = number of partitions of n
Cette page	http://villemin.gerard.free.fr/Referenc/Prof/APROF/Partiti1.htm