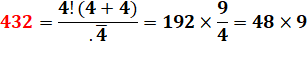|
Édition du: 06/05/2025 |
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||||||||
|
|
|
Un
nombre à trois chiffres avec le même écart entre eux. Divisé par la somme de
ses chiffres, on trouve 48. Diminué de 198, on trouve son retourné. Quel
est ce nombre ? |
![]()
Chiffres et numération
|
432 = 24 × 33 => 2 + 4 + 3 + 3 = 4 × 3 |
Liste: 432, 648, 1152, 4000, 5400, 8748, 9000,
… |
|
432 –
(4 + 3 + 2) = 423 |
|
|
432 |
|
|
432 + 234 = 666 = T36 |
|
|
432
/ (4 + 3 + 2) = 48 432
/ (4 × 3 ×
2) = 18 |
|
|
432 = 24 × 18 |
|
Addition
et soustraction
|
432 = 44 + 33 + 333 +
22 |
|
|
432 = 3 + 4 + … + 29 |
|
|
432 = 103 + 107 + 109 +
113 |
|
Multiplication et division
|
432 = 24 × 33 |
Nombre d’Achille |
|
|
{4, 3, 2} | 432 |
|
|
|
Facteurs de 432
= {2, 3} + 8 =>
{10, 11} qui divisent 432 + 8 = 440 |
|
|
Avec les
puissances
|
432 =
4² + 4² + 20² = 3 × 12² |
|
|
432 =
63 + 63 = 2 x 216 = 23 + 33 + 33
+ 33 + 73 |
Somme de quatre cubes consécutifs toujours
divisible par 2(2n+3) = 2 (2x3+3) = 18. |
En puissance
|
Voir Nombres
p-adiques |
|
|
432² + 576² = 720² 432 + 576 + 720 =
1728 = 123 |
Liste: [54, 72, 90, 6], [192,
756, 780, 12], [200, 375, 425,
10], [270, 704, 754, 12], [343, 1176, 1225, 14], [432, 576, 720, 12], >>> |
Dénombrement, jeux et curiosités
|
|
|
|
|
Avec
la notation anglaise: .4 = 0,4 = 2/5 |
Autour du
nombre
|
432! |
Liste: 432, 444n 453,
458, 474, 476, 485, 489, 498, … |
![]()
|
Question Un nombre à trois
chiffres avec le même écart entre eux. Divisé par la somme de ses chiffres,
on trouve 48. Diminué de 198, on trouve son retourné.
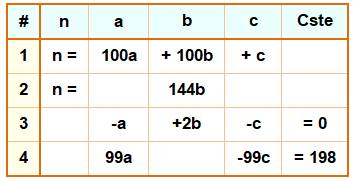
Quel est ce nombre ? Réponse: quatre équations pour
quatre inconnues 100a
+ 10b + c – 198 = 100c + 10b + a => 99a – 99c = 198 => a – c = 2 b
= (a + c) / 2 => 2b = a + c =>
2b = a + a – 2 => b = a – 1 n
/ (a + b + c) = n / 3b = 48 => n = 144b = 144a – 144 Nombre
avec a de 1 à 5: 0, 144, 288, 432, 576 Seul
432 obéit à la décroissance voulue des
chiffres. Sinon,
on aurait pu poursuivre avec la première équation: n
= 100a + 10(a – 1) + (a – 2) = 111a –
12 = 144a – 144 Ce
qui donne: 33a = 132 => a = 4. Système d'équations pour information
Cette
disposition aide à y voir plus clair et à choisir la tactique d'approche la
plus simple. |
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2,
[1, 1, 0, 1, 1, 0, 0, 0, 0] 3,
[1, 2, 1, 0, 0, 0] 4,
[1, 2, 3, 0, 0] 5,
[3, 2, 1, 2] 6, [2, 0, 0, 0] 7,
[1, 1, 5, 5] 8,
[6, 6, 0] 9,
[5, 3, 0] 10, [4, 3, 2] 11, [3, 6, 3] |
12, [3, 0, 0] 13,
[2, 7, 3] 14,
[2, 2, 12] 15,
[1, 13, 12] 16,
[1, 11, 0] 17,
[1, 8, 7] 18,
[1, 6, 0] 19,
[1, 3, 14] 20,
[1, 1, 12] 21,
[20, 12] |
22,
[19, 14] 23, [18, 18] 24,
[18, 0] 25,
[17, 7] 26, [16, 16] 27,
[16, 0] 28,
[15, 12] 29,
[14, 26] 30,
[14, 12] 60,
[7, 12] |
23,
[18, 18] 26,
[16, 16] 35,
[12, 12] 47,
[9, 9] 53,
[8, 8] 71,
[6, 6] 107,
[4, 4] 143,
[3, 3] 215,
[2, 2] 431,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Retour Suite |
|
|
Voir |
|
|
Voir |
![]()