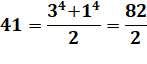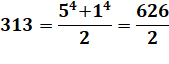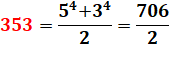|
Édition du: 05/04/2025 |
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||||||||
|
|
![]()
Chiffres et numération
|
353 |
232,
252, 272, 323, 353, 373, 525, 535, 575,
727, 737, 757. |
|
|
353 × (3 + 5 + 3) = 3883 |
|
|
|
353 |
|
|
Addition
et soustraction
|
353 = 13 + 17 +
19 + 23 + 29 +
31 + 37 + 41 +
43 + 47 + 53 |
|
Multiplication et division
|
353 est
premier comme 35353 355 = 5 x 71 |
|
|
3, 5, 33, 35, 53, 335, 353, 533 |
|
|
353, 53, 3 |
|
Les divisions par 353 sont périodiques d'ordre 11
|
La division par 353 des nombres de 1 à 352 produit onze types
de suites périodiques à 32 chiffres et leur permutation. Le nombre premier 353
est le plus petit produisant des fractions d'ordre 11. Avec d'autres numérateurs, on retrouve les mêmes décimales,
éventuellement en permutation
circulaire, précédées d'une partie fixe. Voir exemple avec 1000/353. |
|
Avec les
puissances
|
353 =
8² + 17² = 64 + 289 |
|
|
353 =
24 + 34 + 44
= 8² + 17²
= 177² – 176² = 177 + 176 |
|
|
353 =
(54 + 34) / 2 |
|
|
353 =
|74 – 211|En valeur absolue |
Voir Nombre1999 |
En puissance
|
3534 = 304 +
1204 + 2724 + 3154 |
Voir Nombre 651. |
|
|
Anglais: half-quartan
prime. Le plus petit étant
41. Liste: 41, 313, 353,
1201, 3593, 4481, 7321, 8521, 10601, 14281, 14321, 14593, 21601, 26513, … |
![]()
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2,
[1, 0, 1, 1, 0, 0, 0, 0, 1] 3,
[1, 1, 1, 0, 0, 2] 4,
[1, 1, 2, 0, 1] 5,
[2, 4, 0, 3] 6,
[1, 3, 4, 5] 7,
[1, 0, 1, 3] 8,
[5, 4, 1] 9, [4, 3, 2] 10, [3, 5, 3] 11,
[2, 10, 1] |
12,
[2, 5, 5] 13, [2, 1, 2] 14,
[1, 11, 3] 15,
[1, 8, 8] 16, [1, 6, 1] 17,
[1, 3, 13] 18,
[1, 1, 11] 19,
[18, 11] 20,
[17, 13] 21,
[16, 17] |
22,
[16, 1] 23,
[15, 8] 24,
[14, 17] 25,
[14, 3] 26,
[13, 15] 27,
[13, 2] 28,
[12, 17] 29,
[12, 5] 30,
[11, 23] 60,
[5, 53] |
352,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Retour Suite |
|
|
Voir |
|
|
Voir |
![]()