NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/04/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres	DicoNombre NOMBRES					Glossaire Nombres
1 10 100 1000 5000 10 000 11 000	15 000 à 19 999					20 000 50 000 100 000 10^6 10^9 10^100
	Quinze mille Anglais: Fifteen thousand
15 000		16 000	17 000	18 000	19 000

Pour quinze mille francs mon psychiatre m'a débarrassé de ce que j'avais: quinze mille francs – Coluche

Voir Pensées & humour / Euros

15 000

Économie	15 000 $ Valeur du bitcoin en décembre 2017. Record historique après un bon de 50% en une semaine. Le bitcoin est une monnaie virtuelle apparue en 2008 et qui ne valait que quelques cents. Valeur en 2017: 1000 dollars.
Religion	15 000 paroisses (environ) en France en 2006.	Clergé
Transport	15 349 km entre New-York et Singapour. Plus long vol possible en km (19 h de vol). Hors contrainte de non-survol d'un pays comme la Russie.	Avions

15 000 = 5^6 – 5^4	Différence de puissances de 5.
15 107, 15 121, 15 131	Triplet de premiers pointés; on passe au suivant en ajoutant les chiffres du précédent.
15 120 = 2^4 × 3^3 × 5 × 7	Hautement composé: 80 diviseurs.
15 333 = 1^4 + 2^4 + … 9^4	Somme des bicarrés des nombres de 1 à 9.
15 376 = 124² = 20² + 24² + 120² = (25 – 5)² + (25 – 1)² + (125 – 5)² = (125 – 1)²	Carré somme de trois carrés, différences de nombres en progression géométrique (1, 5, 25, 125). Propriété générale.
		Division curieuse avec les chiffres de 15 501 le seul à cinq chiffres. Avec une coquetterie en 252.
151 15551 155…55121 Chiffres	Nombres rep2digit premiers.
15 613^3 = 33^8 + 1 549 034^2	Puissance = somme de puissances.
15 621	Énigme du singe et des noix de coco.
15 625 = 125^2 = 25^3 = 5^6	Puissance Cube et carré à la fois.
15 625 = 25^3 = 75² + 100² = 44² + 117² = 35² + 120²	Cube somme de deux carrés.
15 625 = 25^3 et 1 = 1², 5 625 = 75²	Cube concaténation de deux carrés.
15 628 = 4 x 3 907 15 678 = 39 x 402	Le plus petit produit pannumérique à 10 chiffres, et le suivant.
15 642 = 1 + 5^6 + 4^2	Nombre de Friedman.
15 750 = 5^3 + 25^3 = 525 (5 + 25)	Somme de deux cubes avec coquetterie.
15 803 = 2^3 + 3^3 + 5^3 + 7^3 + 11^3 + 13^3 + 17^3 + 19^3	Somme des cubes de huit premiers consécutifs.
15 842	Nombre S-parfait.
15 843 × 7 × 1 = 111 111 15 843 × 7 × 2 = 222 222 …	Production de repdigits. Les multiples sont évidemment en progression arithmétique.
15 999, 269, 121, 6, 36, 45, 41, 17, 50, 25, 29, 85, 89, 145, 42, 20, 4	Cycle itératif (somme des carrés des chiffres) record jusqu'à au moins 1 million.

16 000

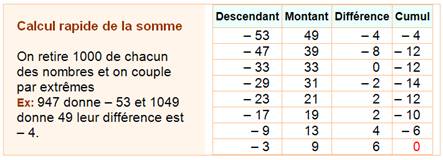
16 000 = 947 + 953 + 967 + 971 + 977 + 983 + 991 + 997 + 1009 + 1013 + 1019 + 1021 + 1031 + 1033 + 1039 + 1049	Somme de 16 nombres premiers consécutifs.
16 038 = 27 x 594 1 368 = 24 x 57	La troisième plus petite multiplication pannumérique à 10 chiffres, suivi de la plus petite à 9 chiffres.
16 091	Nombre premier réversible (strobogrammatique).
16 161 = 5381 + 5387 + 5393	Palindrome somme de trois premiers consécutifs. Trouvé par Olivier D.
16 106 = 8 + 2 ?	Énigme sur le Net.
16 384 = 128^2 = 4^7 = 2^14	Puissance de 2.
16 384 = 4^7 = 8^4 + 8^4 + 8^4 + 8^4 = 4x8^4 = 2^2.2^12 = 2^14 = 4^7		Objet de la question suivante: Résoudre: B.A^3 = B^X
			Puissances avec les chiffres de 2^14.
16 447	Le 10 000^e nombre sans carré.
16 580 = 2^14 + 14^2	Nombre Leyland.
16 641 = 129² et 16 = 4², 4 = 2², 1 = 1²	Carré concaténation de trois carrés (2^e).

16 661 est le 1 928^e premier et 1+6+6+6+1 = 1+9+2+8	Curiosité (G. L. Honaker)
6 661, 16 661, 26 669 …	Nombre premier avec 666. Le plus petit et les suivants. Notez la similitude des deux plus petits.
1 666 1 1 013 666 013 1 = 1000000000000066600000000000001		Le premier palindrome bestial de la forme 1[0...0]n 666 [0...0]n 1 Le suivant est en n = 13 La suite pour n = {0, 13, 42, 506, 608, 2472, et 2623} – Harvey Dubner (Ingénieur électricien et mathématicien américain). Cliff Pickover remarque que dans ce grand nombre premier le nombre de la Bête est entouré de 13 zéros, un nombre de superstition
16661 166..66113 / 17 / 19		Nombres rep2digit premiers avec respectivement: 5, 13, 17 et 19 chiffres.

16 739 = 1^2 + 2^3 + 3^4 + 5^6 + 6^7			Nombre hypertriangulaire-plus.
16 756 = 2^2 + 3^2 + 5^2 + 7^2 + … + 59^2	Somme des carrés de 17 premiers consécutifs.
16 763, 16 787, 16 811	Nombre premier équilibré: même écart (24) avec ses deux voisins. Record. Prochain pour un écart de 30 avec 63 623
16 782 x 4 = 67 128	Mêmes chiffres pour son quadruple avec chiffres uniques (le plus petit à cinq chiffres).
16 807 = 7^5	Ses diviseurs sont: 1, 7, 49, 343, 2 401, 16807
16 830^3= 1134^3 + 1135^3 + 1136^3 + … + 2133^3 = 4 767 078 987 000	Cube, somme de 1000 (= 10^3) cubes consécutifs. 20^3 & 16830^3 sont cités page 345 du livre "Code to Zero" de Ken Follet
16 900 = 130²	Nombre Carré Voir Curiosité avec ce nombre
Div(16 999) = {1, 89, 191, 16 999} 89 + 191 = 280 et 1²+6²+9²+9²+9² = 280		Somme des diviseurs non-triviaux égale à la somme des carrés des chiffres. Nombre canadien parfait. Ils sont quatre à partager cette propriété: 125, 581, 8 549 et 16 999.

17 000

Physique

17 000 Hz = 17kHz Ultrason pleinement audible par les jeunes de moins de 20 ans. Inaudible au-delà de 30 ans. Cette propriété a été mise à profit dans deux cas d'application: 1) Le produit Mosquito, dispositif sonore qui, placé devant un magasin, devait faire fuir les bandes de jeunes gêneurs. 2) Sonnerie de téléphone pour s'appeler entre jeunes (Échanges de SMS / Texto en classe!). L'Express – 13/7/2006

Son

Nombre	17 160 = 10×11×12×13	Bases 2, [1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0] 3, [2, 1, 2, 1, 1, 2, 1, 2, 0] 4, [1, 0, 0, 3, 0, 0, 2, 0] 5, [1, 0, 2, 2, 1, 2, 0] 6, [2, 1, 1, 2, 4, 0] 7, [1, 0, 1, 0, 1, 3] 8, [4, 1, 4, 1, 0] 9, [2, 5, 4, 7, 6] 10, [1, 7, 1, 6, 0] 11, [1, 1, 9, 9, 0] 12, [9, 11, 2, 0] 13, [7, 10, 7, 0] 14, [6, 3, 7, 10] 15, [5, 1, 4, 0] 16, [4, 3, 0, 8]
Facteurs
Diviseurs	1, 2, 3, 4, 5, 6, 8, 10, 11, 12, 13, 15, 20, 22, 24, 26, 30, 33, 39, 40, 44, 52, 55, 60, 65, 66, 78, 88, 104, 110, 120, 130, 132, 143, 156, 165, 195, 220, 260, 264, 286, 312, 330, 390, 429, 440, 520, 572, 660, 715, 780, 858, 1144, 1320, 1430, 1560, 1716, 2145, 2860, 3432, 4290, 5720, 8580, 17160
Quantité	64
Somme	60 480
S - N	43 320

17 160 = 10 x 11 x 12 x 13	Factorielle tronquée. Divisible notamment par 4! = 24.
17 163	Tous les nombres au-delà sont la somme de deux premiers distincts au carré.
17 280	Comporielle.
17 280 = 416008 = 4! x 1! x 6! x 0! x 0!	Nombre égal au produit des factorielles de ses chiffres en base 8.
17 296 & 18 416	Paire de nombres amiables. Deuxième paire connue. Fermat 1636.
17 576 = 26^3 = 74² + 110² = 26² + 130²	Cube somme de deux carrés.
17 576 = 26^3 26 = 1 + 7 + 5 + 7 + 6	Nombre de Dudeney.
17595 + 18 = 17613 17595 x 18 = 316710	Motif unique avec 18.
17 642 42 x 42 = 1 764	Un des deux nombres avec 86 493 à présenter ce motif avec des chiffres différents.
17 764 = 2^4 + 3^4 + 5^4 + 7^4 + 11^4	Somme des puissances 4 de cinq premiers consécutifs.
17 711	Nombre de Fibonacci avec répétition de chiffres.

Littérature

17 913 vaches – Gargantua – Rabelais – 1534 On amena dix-sept mille neuf cent treize vaches, car le lait de la reine, la géante Gargamelle, ni celui d'aucune nourrice du royaume ne pouvait suffire à apaiser la soif du nouveau-né. Chaque jour, Gargantua gagnait en force et en taille. Il avait une bonne tête ronde prolongée par dix-huit mentons bien gras.

Romans Pantagruel

18 000

Défense

18 000 têtes nucléaires dans le monde vers 2000

>>>

18 181	Nombre premier réversible de plusieurs façons: palindrome, strobogrammatique, tétradique et dihédral >>> Le précédent: 181 Le suivant: 1008001 Nombre premier ondulant en 1 et 8. Le suivant a 77 chiffres.
18 431 ≠ 2^a٠3^b + 2^c٠3^d + 2^e٠3^f + 2^g٠3^h	Plus petit nombre non représenté par cette forme dite double-base avec seulement quatre termes.
18 432 = (1×8)^3 + (2×8)^3 + (3×8)^3	Somme de cube dans le ratio1, 2 et 3. Liste: 36, 288, 972, 2304, 4500, 7776, 12348, 18432, 26244, 36000, 47916, 62208, 79092, 98784, 121500, 147456, 176868, 209952, 246924, 288000, …

Économie

18 500 € / m² Loyer moyen à New York, 5^e Avenue en 2010 14 600 Hongkong, Causeway Bay 7 700 Tokyo, Ginza 7 350 Londres, New Bond Street 7 000 Paris, Champs Élysées L'Expansion – Novembre 2010

>>>

18 600	Nombre à moyenne harmonique entière.
18 700 = 1^7 + 2^7 + 3^7 + 4^7	Somme de puissance des nombres. Divisible par le nombre suivant 5; propriété générale.
18 751^2 = 351 600 001	Puissance entière terminée par 00001.
18 785 = 4^7 + 7^4	Nombre Leyland.

Économie

18 857 euros par habitant en France en 2016 Montant de la dépense d’État : sécurité, éducation, santé, logement, famille … 11 663 en 1996, soit 62 % d’augmentation. 16 787 en 2016 en Allemagne, soit 11% en moins ; alors que la richesse par habitant est 13% plus faible en France.

18 980 = 2² × 5 × 13 × 73 = 52 × 365

Facteurs avec quantité de semaines en un an et quantité de jours.

19 000

19 091 = 171819 / 9	Palindrome formé avec trois nombres successifs. Ce type de nombre est toujours divisible par 9. Coquetterie avec le 19.
19 321 = 139² x 1	Opération avec ses chiffres.
19 513	Nombre tribonacci.
19 521	Nombre 2-hyperparfait.

19 600 = 2^4 x 5² x 7² = 140² = 1+3+6+10+15+...+1176	Nombre carré et tétraédral, le seul, mis à part 4 = 2² = 1 + 3.
= 3^3 + 18^3 + 24^3 = 1^3 + 3^3 + 2 x 6^3 + 2 x 8^3 + 10^3 + 11^3 + 2 x 12^3 + 13^3 + 14^3 + 15^3 + 16^3	Puissance. Plus grand nombre cube Pour mémoire:
19 683 = 10^100 en base 3	Googol en base 3. Car 103 = 3 et 1003 = 9.
27 = 1 + 9 + 6 + 8 + 3 19 683 = 1 + (9 – 6)^8 x 3	Nombre de Dudeney. Le plus grand cube. Nombre de Friedman.

19720 = 42² + 134² = 82² + 114² = 26² + 138² = 62² + 126² 19 721 = 35² + 136² = 20² + 139² = 64² + 125² = 11² + 140²	Deux nombres consécutifs, somme de 2 carrés 4 fois Voir nombre, sommes de carrés
19 855 = 55² + 56² + 57² + 58² + 59² + 60² = 61² + 62² + 63² + 64² + 65²		Somme de six carrés = somme de cinq carrés, tous consécutifs. Seule solution.

Somme de carrés consécutifs

Écrire des deux sommes:

Développement de ces deux expressions:

A = 6n² – 30n + 55

B = 5n² + 30 n + 55

Égalité:

n² = 60 n et n = 0 ou 60

Généralisation Voir Somme de nombres consécutifs

Précédent: 7 230 ; Suivant: 45 955

19 861	Nombre premier réversible (strobogrammatique).
191 19991 199999991	Nombres rep2digit premiers.

Suite	Nombres 20 000
Voir	Nombre Chanceux Semaine Palindrome Triangle Tectroèdre Raisonnement Rep Unit Suites Nombre Têtus
Cette page	http://villemin.gerard.free.fr/NombDico/N1000/N15000.htm

Quelques repères dans ces pages

>>> SOMME DE PREMIERS

>>> PALINDROME BESTIAL

>>> PUISSANCE

>>> CUBES

>>> CARRÉS

>>> SOMME DE PREMIERS CARRÉS

>>> AMIABLE - PAIRE

>>> CARRÉ ET TÉTRAÉDRIQUE

>>> SOMME DE CARRÉS 4 fois

>>> ULTRASON

>>> TÊTES NUCLÉAIRES