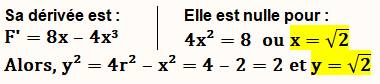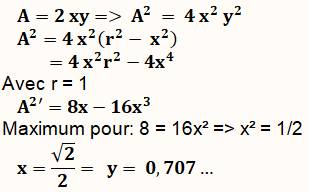NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/01/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométrie
Débutants Géométrie	Rectangles et disques				Glossaire Géométrie
INDEX Construction Géométrie	Cercles dans le rectangle		Densité de disques	Empilement des sphères
	Rectangle dans le cercle
		Sommaire de cette page >>> Approche 1 – Aire du triangle >>> Approche 2 – Aire du rectangle

Voir Propriétés fondamentales des triangles

Rectangle dans le cercle

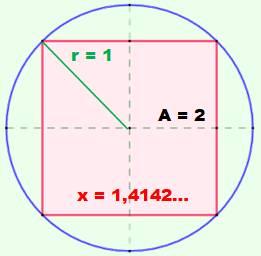
Taille du rectangle le plus grand dans le cercle.

Sans surprise, il s'agit du carré.

Son côté mesure et l'aire vaut 2 r².

Deux approches: aire d'un triangle élémentaire ou aire du rectangle.

Anglais: Finding the Largest Rectangle

Approche 1 – Aire du triangle
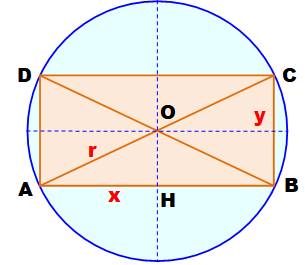
Position du rectangle On suspecte que le plus grand rectangle intérieur à un cercle est le carré inscrit centré sur le centre du cercle. Encore faut-il le montrer. On comprend que le rectangle doit être totalement inscrit dans le cercle (sommet sur la circonférence). On augmente l'aire du rectangle en le centrant sur le cercle. De toute façon, il est automatiquement placé de la sorte en étant inscrit dans le cercle.

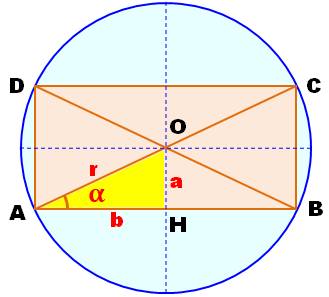
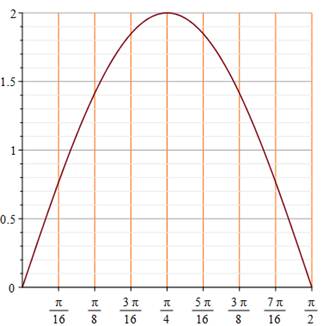
Aire maximale – Graphe L'aire du rectangle est une fonction de l'angle alpha (le rayon r est une constante). Son graphe, pour un angle variant de 0 à 90°, montre un sommet (maximum) pour un angle de 45°, soit le double pour l'angle entre les diagonales. Un rectangle dont les diagonales se coupent à angle droit est un carré.	Pour r = 1: A = 4 sin cos
Aire maximale – Calcul La fonction A atteint un maximum lorsque sa dérivée A' est nulle. La dérivée d'un produit uv est (uv' + u'v) Dérivée du sin = cos, et celle du cos = – sin.	A' = 0 pour sin = cos qui représentent les côtés du triangle jaune; ce qui induit a = b. Le rectangle est un carré.

Approche 2 – Aire du rectangle
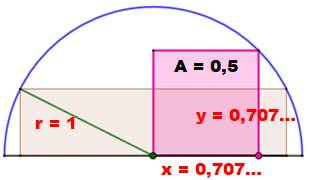
Dans le cercle On s'intéresse directement au carré de l'aire du rectangle. Sans perte de généralité pour calculer le maximum, prenons r = 1. Il s'agit de maximiser: Le rectangle d'aire maximale est un carré.
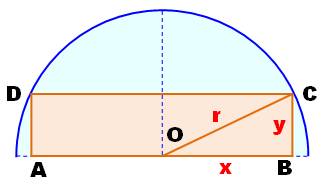
Dans le demi-cercle Cette fois, le rectangle est placé dans le demi-cercle. La résolution est identique. Conclusion: ce sont deux solutions identiques: l'une moitié de l'autre. L'aire du carré complet dans le cercle est égale à 4 x 0,5 = 2.

Suite	Cerces dans le rectangle Densité de disques Empilement des sphères
Voir	Cercle DicoMot Losange et son cercle inscrit Sangakus Triangle – Index Triangles et carrés
Site	Determining the largest rectangle which can be inscribed in a circle – Animation Geogebra
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/RectCerl.htm