|
Édition du: 09/02/2025 |
|
INDEX |
Rectangles et disques |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Rectangle évidé par des cercles |
||
|
|
Sommaire de cette page >>> Rectangle, quart et demi-cercles >>> Rectangle évidé par des cercles |
Débutants Glossaire |
|
Problème très simple à condition de ne pas s'embarquer dans des calculs
trop tôt. |
||
|
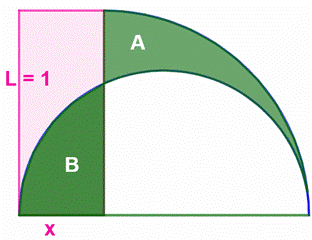
Construction Un
rectangle de dimensions (L et x). Un quart
de cercle construit sur sa longueur et un demi cercle tel que montré sur la
figure. Quelle est
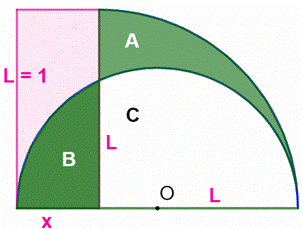
la valeur de x pour que les aires A et B soient égales ? Pistes Notons C
la zone circulaire blanche : Nous
devons obtenir A + C = B + C, avec C commun aux deux côtés de l'égalité. Calculs Aires : En comparant
les égalités (fois 8 pour faciliter les calculs): |
Figure initiale avec L = 1
Figure avec notations
|
|
|
Comment résoudre ce problème de géométrie où une seule mesure est connue ?
Se souvenir qu’en un point de tangence, le rayon du cercle est
perpendiculaire à la tangente. Alors, si deux rayons aboutissent au même
point de tangence, ils sont situés sur la même droite. |
||
|
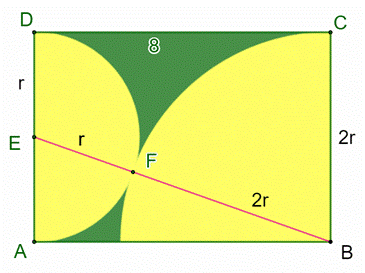
Construction Un rectangle
dont le grand côté mesure 8 cm. Un demi
cercle est tracé avec le petit côté comme diamètre. Un quart de cercle occupe
la partie droite du rectangle. Quelle est
l’aire de la zone verte ? Calcul de r (Voir la figure du bas) Nommons r le
rayon du demi-cercle ; celui du quart de cercle sera égal à 2r. Si F est
le point de tangence des deux cercles, EF est un rayon et BF aussi pour
l’autre cercle. Ces deux rayons sont colinéaires. Les points E, F et B sont
alignés. Avec le
théorème de Pythagore dans le triangle rectangle ABE : Calcul de l’aire Aire du
rectangle : 8 × 2r = 16r Aire du
demi-cercle : 1/2 π r² Aire du
quart de cercle : 1/4 π (2r)² = π r² Aire
verte : A = 16r – 3/2 π r² Avec r² =
8 = 2√2 |
Figure initiale
Figure avec notations
|
|
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/CercReEv.htm
|