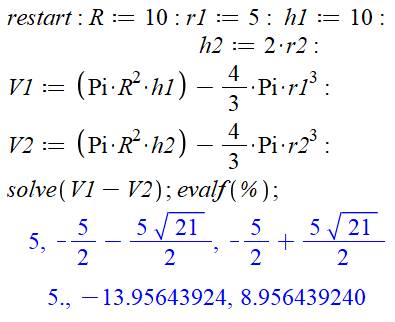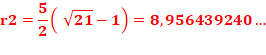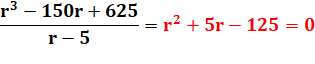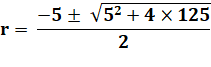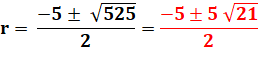|
||||||||||||||||||||||||||||||||
![]()
|
CYLINDRE et BOULES pour le même niveau d'eau Problèmes typiques de la classe de seconde. Où il est question d'une équation du
troisième degré que l'on va résoudre selon quatre méthodes (dont 3
accessibles en classe de seconde). |
|
|
||
|
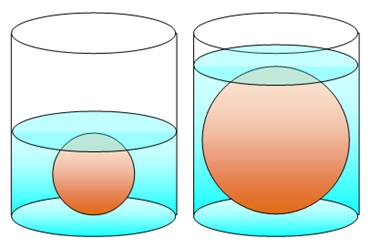
Problème Un cylindre:
R = 10 cm et H = 22 cm. Une boule: r1 = 5
cm. On verse
de l'eau
jusqu'à recouvrir exactement la boule (lourde). On retire la boule tout en
conservant l'eau. Une
seconde boule de rayon r2 inconnu. Mise dans le cylindre, l'eau
affleure le haut de la boule. Quelle
est la valeur de r2, le rayon de la seconde boule? |
|
|
|
Observations À lire
l'énoncé, on aurait tendance à penser qu'il n'y a pas de problème: c'est la même
boule qui déplace le même volume d'eau. N'est-ce pas? Eh bien non! Une boule plus grosse va
"resserrer" l'eau sur les côtés. Les filets sur les bords seront de
plus en plus minces avec une boule de plus en plus grosse; l'eau va remonter
plus haut. On nous demande la taille de la boule si on a la
même quantité d'eau que dans l'expérience initiale. |
Conclusions à ce stade Le volume
d'eau est le même dans les deux cas: c'est la différence entre le volume du
cylindre en eau, diminuée du volume de la boule. La
hauteur du cylindre en eau est égale au diamètre de la boule. Méthode de calcul 1) On a tous les paramètres pour calculer le
volume d'eau dans le cas de l'expérience 1. 2) On ne connait pas r, le rayon de la boule,
dans le cas de l'expérience 2, il faut le calculer à partir de la
connaissance du volume d'eau. |
|
|
|
|||
|
Première boule: |
r1 = 5 et h1
= 10 |
||
|
Volume de
l'eau = volume
du cylindre en eau – |
|
||
|
Deuxième boule |
r2 = ? et h2 = 2r2 |
||
|
Volume du
cylindre en eau: volume de
la boule en eau: volume de
l'eau: |
|
||
|
Égalité des
volumes d'eau En
multipliant l'égalité par 3 et en divisant par 4. Puis en
divisant par Pi. |
|
||
|
La résolution de cette équation donne trois racines. |
5; 8, 956;
–13,95 |
||
|
On
retrouve la solution initiale Une
nouvelle valeur apparaît La
troisième, négative est à rejeter |
r1 = 5 cm r2 = 8,956 cm r3 = -13,95 cm |
||
|
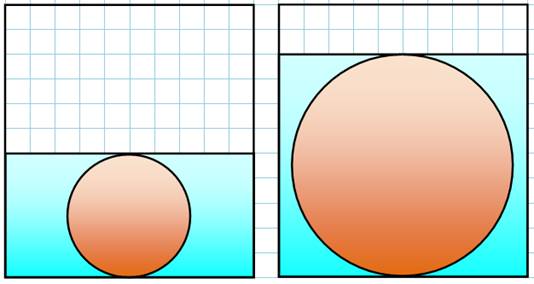
Représentation
des deux boules dans le récipient à l'échelle avec 1 carreau = 2 cm Les
deux volumes d'eau en bleu sont égaux.
Rappel:
récipient cylindrique de 10 cm de rayon (10 carreaux sur le dessin). et de 22 cm de hauteur
(cette donnée ne sert à rien sinon à dire que le récipient est assez grand
pour contenir l'une des deux billes. |
|
|
||
|
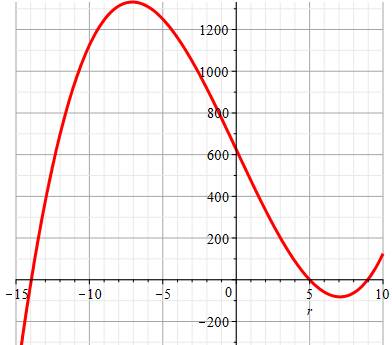
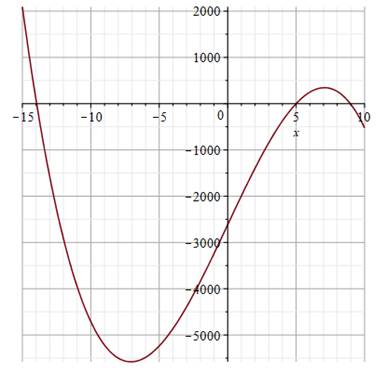
Méthode 1 – Graphique Seule
méthode du niveau de la classe de seconde Graphe de
la fonction y = r3
– 150 r + 625 => On relève
les trois racines (là où la courbe coupe l'axe des x; c'est-à-dire pour y =
0). On retient
r voisin de 9. |
|
|
|
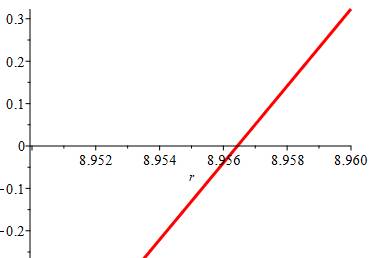
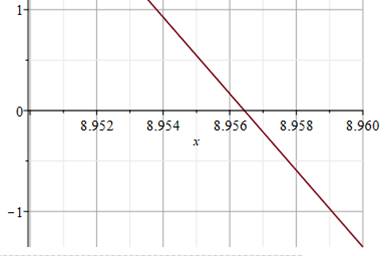
Focalisation sur la racine voisine
de 9 Zoom pour
x entre 8,95 et 8,96 pour lire une valeur plus précise. On lit: r2
= 8,956 … |
|
|
|
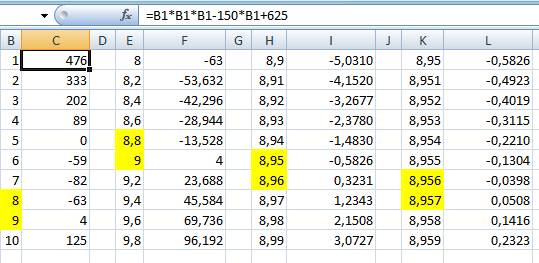
Méthode 2 avec tableur et
approximations successives La formule est introduite (exemple pour C1) En jaune, le changement de signe qui indique que la
racine est dans cette plage Chaque groupe de deux colonnes montre un affinage
progressif de la solution.
|
|
Méthode 3 avec calculette ou
logiciel de calcul
|
Commentaires On réinitialise les calculs (toutes les variables
d'un calcul précédent sont effacées). Introduction des valeurs connues. Formule
de calcul pour les deux volumes V1 et V2 correpondant aus deux boules. Demande
de résolution (solve) de l'équation V1 = V2, sachant que seul r2
est inconnu. En
bleu, résultat du cacul, d'abord sous forme avec radicaux, puis sous forme
numérique. Nous
disposons de la valeur exacte r2:
|
|
Méthode 4 avec résolution de
l'équation (hors programme de seconde) |
r3 – 150 r + 625 = 0 |
|
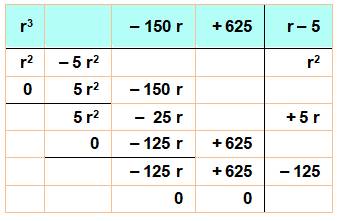
On dispose d'un atout: on sait que 5 est une racine,
ce qui veut dire que ce polynôme est divisible par (r – 5). On effectue la division du
polynôme comme s'il s'agissait d'une division de nombres. |
|
|
On a donc: |
|
|
Résolution de l'équation
du deuxième degré: |
|
![]()
Pour
information: résolution avec les valeurs numériques
Qui montre que l'on peut
se compliquer un poil la vie en voulant aller au but trop directement
|
Calcul du rayon de la boule |
|
||
|
Première boule: |
r1 =
5 et h1 = 10 |
||
|
Volume du
cylindre en eau: Volume de
la boule: Volume de
l'eau: |
Vc = pi . R² . h1 = 3,14 x 10² x 10 =
3141,59 cm3 Vb = 4/3 pi . r13
= 4/3 x 3,14 x 53 = 523,60 cm3 Ve = Vc – Vb =
2618 cm3 |
||
|
Deuxième boule |
r2 =
? et h2 = 2r2 |
||
|
Volume du
cylindre en eau: Volume de
la boule: Volume de
l'eau: |
Wc = pi. R². h2 = 3,14 x 10² x 2r2
= 628,32 r2 Wb = 4/3 pi . r23 = 4/3 x 3,14
x r23 = 4,188 r23 We = Wc – Wb = 628,32 r2 – 4,188 r23
|
||
|
Égalité
des volumes d'eau |
628,32 r2
– 4,188 r23 = 2618 |
||
|
La résolution de cette équation donne trois racines |
5; 8, 956;
–13,95 |
||
|
On retrouve
la solution initiale Une
nouvelle valeur apparaît La
troisième, négative est à rejeter |
r1 = 5 cm r2 = 8,956 cm r3 = -13,95 cm |
||
|
|
||
|
Méthode1 – Graphique Seule
méthode du niveau de la classe de seconde Graphe de
la fonction y = 628,32 x – 4,188 x3 – 2618 => On relève
les trois racines (là où la courbe coupe l'axe des x; c'est-à-dire pour y = 0).
|
|
|
|
Focalisation sur la racine voisine
de 9 Zoom pour
x entre 8,95 et 8,96 pour lire une valeur plus précise. On lit: r2
= 8,956 … |
|
|
|
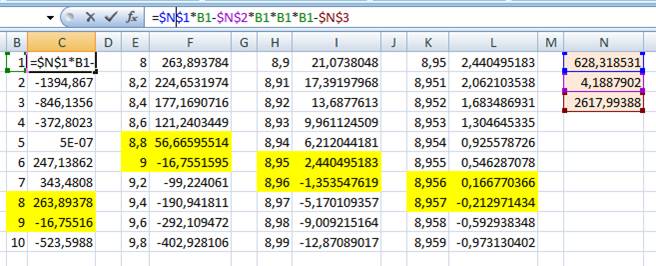
Méthode 2 avec tableur et
approximations successives La formule est introduite en prenant les valeurs
des paramètres dans la colonne N En jaune, le changement de signe qui indique que la
racine est dans cette plage Chaque groupe de deux colonnes montre un affinage
progressif de la solution.
|
|
Méthode 3 avec calculette ou
logiciel de calcul
|
Commentaires On réinitialise les calculs (toutes les variables
d'un calcul précédent sont effacées). Introduction des valeurs connues. Formule
de calcul pour les deux volumes V1 et V1 correpondant aus deuxboules. Demande
de résolution (solve) de l'équation V1 = V2, sachnat que seul r2
est inconnu. En
bleu, résultat du cacul, d'abord sous forme aves radicaux, puis sous forme
numérique. Nous
disposons de la valeur exacte r2:
|
![]()
|
Retour |
|
|
Aussi |
|
|
Cette page |
![]()