NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/11/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Calcul mental
Débutants Général	RACINE CARRÉE			Glossaire Général
INDEX Racine carrée Calcul	Deux chiffres	Trois chiffres	"Recette"
		Sommaire de cette page >>> Méthode avec exemple

Algorithme de

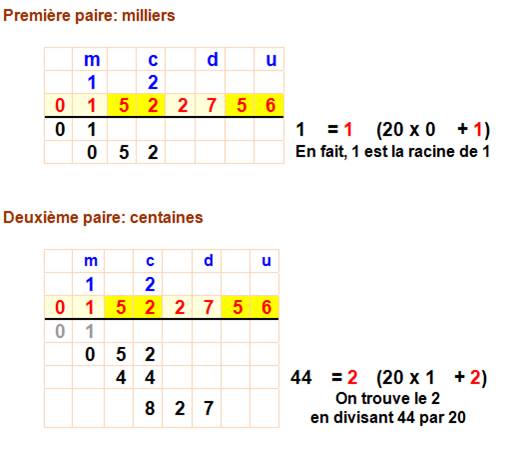
CALCUL d'une RACINE CARRÉE

Méthode expliquée et raisonnée (analogie géométrique) >>>

Méthode pratique, simplement décrite ci-dessous >>>

Méthode avec exemple: = ?
Initialisation Séparer le nombre en paires. Boucle Départ et notations Abaisser la paire de chiffres de plus grand poids. - Le nouveau nombre est la valeur courante C; - q est le quotient tel qu'il est connu; - x est le nouveau chiffre du quotient; - y = x (20q + x) Calcul Cherchez le plus grand x tel que y < C. Ajouter x dans le quotient Soustraire y de C. Test de boucle Reprendre du début de la boucle s'il reste encore des chiffres à abaisser. Fin de boucle Note Un carré parfait donnera un reste final nul (comme dans notre exemple).

Voir Méthode expliquée

Voir	Calcul des carrés Calcul des racines carrées – Index
Aussi	Nombres carrés Carrés en géométrie
Cette page	http://villemin.gerard.free.fr/Calcul/Operatio/RacCarRe.htm