|
Édition du: 19/11/2023 |
|
INDEX |
Types de Nombres – Motifs |
|||
![]()
|
NOMBRES ab + bc + ca Nombres pavés Nombres O'Halloran Les nombres qui ne sont pas de cette forme
sont sans doute limités à 18 représentants:
|
||
|
|
Sommaire de cette page >>> Approche >>> Définition et liste >>> Propriétés |
Débutants Glossaire |
|
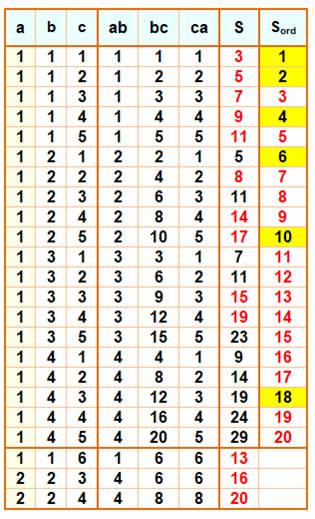
Dressons le
tableau des valeurs de S = ab + bc + ca pour les valeurs successives de a, b
et c. Dans la
colonne S, on met en rouge les nombres dès leur première occurrence et on
reporte cette valeur dans la colonne SOrdonné pour identifier les
valeurs trouvées par ordre croissant. Une
analyse assez courte (jusqu'à 2, 2, 4) révèle que tous les nombres sont
couverts jusqu'à 20, sauf: Une
exploration plus poussée montre que ces six nombres sont résistants: aucune
valeur de (ab + bc + ca) ne peut les atteindre. Ils
constituent le début de la liste des nombres non (ab+bc+ca). |
|
|
|
Les nombres N = ab + bc + ca sont tous ceux qui
sont atteignables par cette formule pour des valeurs de a, b et c positives
(non nulles). |
N = ab + bc + ca {3, 5, 7,
8, 9, 11, 12 …} |
|
|
Les nombres nN = non(ab + bc + ca) sont tous ceux
qui ne sont pas atteignables par cette formule pour des valeurs de a, b et c
positives (non nulles). On pense que cette liste est complète. |
nN = jamais ab + bc + ca {1, 2, 4,
6, 10, 18, 22, 30, 42, 58, 70, 78, 102, 130, 190, 210, 330, 462} |
|
|
Les nombres nN = non(ab + bc + ca) auxquels on
ajoute 1 sont premiers. Tous les nombres, premiers
comme composés,
au-delà de 462 sont accessibles avec la formule ab + ba + ca. |
nN + 1 sont des nombres premiers {2, 3, 5,
7, 11, 19, 23, 31, 43, 59, 71, 79, 103, 131, 191, 211, 331, 463} |
||||
|
Les grands nombres sont accessibles par cette
formules un très grand nombre de fois. Par exemple, six fois pour 463 et vingt fois pour
464. |
463, 1, 3, 115 463, 1, 7, 57 463, 1, 15, 28 463, 3, 5, 56 463, 7, 9, 25 463, 8, 9, 23 |
464, 1, 2, 154 464, 1, 4, 92 464, 1, 14, 30 464, 2, 2, 115 464, 2, 4, 76 464, 2, 7, 50 464, 2, 10, 37 464, 2, 11, 34 464, 2, 16, 24 464, 3, 8, 40 |
464, 4, 4, 56 464, 4, 6, 44 464, 4, 8, 36 464, 4, 11, 28 464, 4, 12, 26 464, 4, 16, 20 464, 6, 14, 19 464, 7, 12, 20 464, 8, 8, 25 464, 8, 14, 16 |
||
|
Nombres pavés Le double des nombres nN représente l'aire totale
des faces d'un pavé de
dimension (a, b, c). S = 2ab + 2bc + 2ca = 2N Conséquence, l'aire des faces ne sera jamais: |
S = 2 (ab + bc + ca) S = aire des faces du pavé, jamais: {2, 4, 8,
12, 20, 36, 44, 60, 84, 116, 140, 156, 204,
260,
380,
420,
660,
924} |
||||
Voir Brève
542
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |