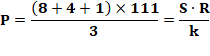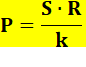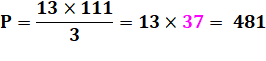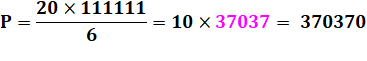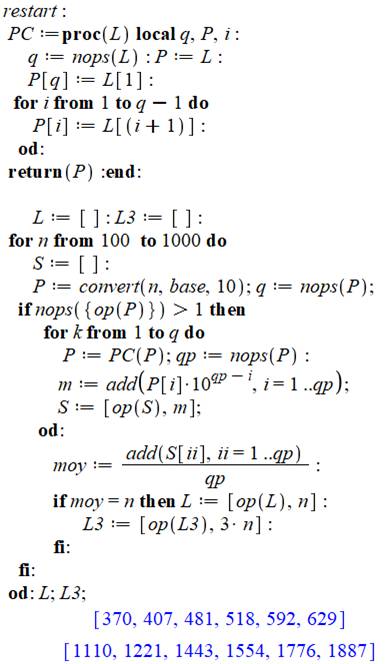|
Édition du: 20/11/2023 |
|
INDEX |
Types de Nombres – Motifs |
|||
![]()
|
NOMBRES PERMUTATIONS Nombres égaux à la moyenne de leurs permutations.
|
||
|
|
Sommaire de cette page >>>
Nombres permutations >>>
Liste
des nombres permutations >>>
Propriétés >>>
Programmation |
Débutants Glossaire |
|
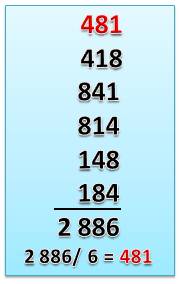
Permutations circulaires (Tableau
de gauche) Ce nombre de trois chiffres produit trois nombres
par permutations
circulaires (déplacement d'un cran des chiffres). La somme vaut 1 443 et, avec trois nombres, la
moyenne est égale = 1 443 / 3 = 481. Cette moyenne est égale au nombre lui-même. Toutes les permutations (Tableau
de droite) En considérant toutes les permutations, on ne
fait que doubler les mêmes chiffres dans chaque colonne. Il tout à fait normal de retrouver la même
moyenne. Quantité de permutations La quantité de permutations circulaires est égale
à la quantité n de chiffre du nombre,
alors que celle de toutes les permutations est égale à n! |
|
||
|
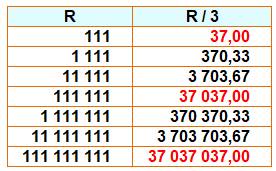
Solutions triviales Avec un nombre comme 111, les permutations
circulaires sont réduites à une. La moyenne est naturellement égale au
nombre. Nous éviterons des nombres appelés repdigits
ainsi que les nombres-chiffres (1, 2, 3…). |
Exemples 1, 2, 3, .. 11, 22, 33, … |
||
Voir Brève 55-1096
|
Liste des nombres permutations Avec cas triviaux |
1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55,
66, 77, 88, 99, 111, 222, 333, 370, 407, 444, 481, 518, 555, 592, 629, 666,
777, 888, 999, 1111, 2222, 3333, 4444, 5555, 6666, 7777, 8888, 9999, 11111,
22222, 33333, 44444, 55555, 66666, 77777, 88888, 99999, 111111, … |
|
|
Originaux (sans cas
triviaux) Après trois chiffres ces nombres présentent un caractère
répétitif. |
370, 407, 481, 518, 592, 629, 370370, 407407, 481481,
518518, 592592, 629629, 370370370,
407407407, 456790123, 469135802, 481481481, 493827160, 506172839,
518518518, 530864197, 543209876, 592592592, 629629629, 370370370370370, 407407407407407, 481481481481481,
518518518518518, … Note: le nombre 456 790 123 est remarquable
car quasi pannumérique
(manque le 8) et il présente deux suites croissantes de trois chiffres. Par ailleurs, il est nouveau. On n'y retrouve pas
une répétition des précédents. |
|
|
Le triple de
ces nombres |
1110, 1221, 1443, 1554, 1776, 1887, 1111110,
1222221, 1444443, 1555554, 1777776, 1888887. Note: les triples présentent un motif uniforme. Les
motifs absents correspondent aux nombres permutations triviaux. |
|
|
Ces nombres sont étroitement liés aux repdigits. La somme des permutations circulaires peuvent se
décomposer comme suit avec l'exemple de 481: La somme peut être arrangée: Et la moyenne devient: |
Formule
Si la somme des chiffres de P = S, alors le nombre est nombre permutation. P = nombre potentiellement "permutation". S = Somme des chiffres de n. k = quantité de chiffres dans n. R = repunit
de k chiffres. Exemple avec 481
|
||
|
Cette expression peut être généralisée. |
Exemple avec 370 370
|
||
|
Avec trois chiffres, le repunit 111 est divisible
par 3 ce qui assure que la moyenne soit un entier. En outre, il est divisible par 37, de sorte que
tous les nombres permutations à trois chiffres sont divisibles par 37. On ne retrouve cette divisibilité par 3 que pour une
quantité de chiffres divisibles par 3. |
|
||
|
Ces huit nombres permutations originales (non
répétition des précédents) sont des fractions
avec 81 pour dénominateur. Note: 10 / 81 = 0,12345679
0123… quasi pannumérique
(manque le 8) comme 456 790 123, un des nombres permutations. On trouve aussi les fractions avec 27 au
dénominateur comme 10/27 = 0,370370… Pour trouver de très grands nombres, on trouvera
des fractions avec 243 au dénominateur et 119 à 125 au numérateur (H.v.
Eitzen) Ou encore 729 avec 361 à 368 au numérateur. |
|
||
|
|
But Lister les nombres permutations originaux. Méthode par examen systématique des nombres
(brut-force method) Commentaires Procédure qui effectue la permutation circulaire
d'un cran sur une liste. Le premier chiffre devient le dernier et exécution
d'une boucle pour faire décaler les suivants. Le programme principal examine les nombres de 100
à 1000 (exemple). Chaque nombre n est convertit en liste de
chiffres avec convert. Une boucle de longueur égale à la quantité de
chiffres effectue les permutations circulaires. Pour chacune le nombre (m)
est restitué à partir de la liste avec add. La liste S est complétée par ces nouvelles
valeurs m. Permutations terminées, on calcule la moyenne des
nombres figurant dans la liste S. Si la moyenne est égale au nombre n initial, la
liste des nombres permutations (L) est complétée. On liste également le triple de ces nombres Remarque Ce programme est très basique. Vous trouverez un
programme optimisé en OEIS A160818. |
||
|
restart; PC := proc (L) local q, P, i; q := nops(L); P := L; P[q] :=
L[1]; for i to q-1 do P[i] := L[i+1] end do; return P end proc: L := []; L3
:= []; for n from 100 to 1000 do S := []; P := convert(n, base, 10); q :=
nops(P); if nops({op(P)}) > 1 then for k to q do P := PC(P); qp :=
nops(P); m := add(P[i]*10^(qp-i), i = 1 .. qp); S := [op(S), m] end do; moy
:= add(S[ii], ii = 1 .. qp)/qp; if moy = n then L := [op(L), n]; L3 := [op(L3),
3*n] end if end if end do: L; L3 |
Listing du programme pour un copier-coller dans Maple |
||
Voir Programmation – Index
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |