NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 17/05/2021

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths

       

Types de Nombres

 

Débutants

Général

Diviseurs

 

Glossaire

Général

 

 

INDEX

 

Types de nombres

 

Somme carrée

Somme cube

Canadiens parfaits

Sigma . Phi = k4

Relations Sigma-Phi

 

Sommaire de cette page

>>> Définition

>>> Liste

>>> Programmation

 

 

 

 

 

Famille

Nombre / Division

Définition

 

Nombre en puissance quatrième (bicarré) qui est égal au produit de sigma par phi

 

Rappel

Sigma est la fonction arithmétique donnant la somme des diviseurs d'un nombre.

 

Phi est le totient ou indicatrice d'Euler. Cette fonction indique la quantité de nombres premiers avec n tout en étant inférieurs à n.

 

 

Liste

 

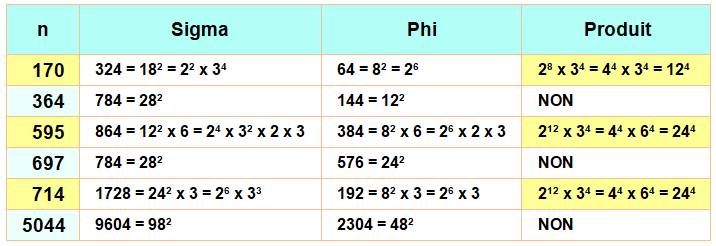
Les plus petits expliqués: 170, 595 et 714

Remarquez que la puissance 4n'est pas liée au carré de sigma et de phi (364, 697, 5044 …)

 

 

 

Liste des 27 plus petits

1, 170, 595, 714, 121056, 480441, 529620, 706063, 706237, 729752, 755972, 815654, 2162808, 2449062, 2827789, 2927848, 2957416, 2994681, 2995419, 3010227, 3019028, 3019772, 3080140, 3093860, 3103464, 3206364, 3213804, …

 

 

 

Programmation

 

Listing du programme pour copie dans Maple

restart; with(numtheory): for n from 2 to 1000 do S := sigma(n); P := phi(n); SS := sqrt(sigma(n)); PP := sqrt(phi(n)); if evalf(S^(1/4)*P^(1/4)) = floor(S^(1/4)*P^(1/4)) then print(n, S, P, SS, PP, sqrt(SS*PP)) end if end do;

 

Commentaires

 

Réinitialisation et appel des logiciels de théorie des nombres.

Boucle de recherche sur n.

Calcul de sigma et phi  et de leur racine carrée.

Recherche du produit dont la racine quatrième est un entier (son développement décimal est égal à son plancher).

 

 

 

En bleu, résultat de la recherche.

Voir Programmation – Index

 

 

 

Suite

*  Bicarrés (puissance quatrième)

*  Carrés

*  Diviseurs

*  Diviseurs somme carrée

*  Diviseurs somme puissance

*  Nombre dont la somme des diviseurs est un carré

*  Relations Sigma-Phi

*  Somme des diviseurs égal bicarrés

*  Tables des sommes de diviseurs  = puissance

DicoNombre

*  Nombre 170

Livre

*  Ces nombres qui nous fascinent - J.-M. De Koninck – Ellipses – 2008.

Site

*  OEIS A114078 – phi(n) times sigma(n) is a fourth power

Cette page

http://villemin.gerard.free.fr/aNombre/TYPDIVIS/SigmaPhi.htm