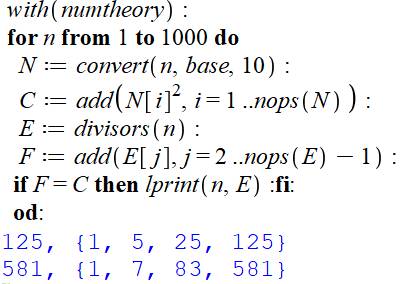|
|||||||||||||||||||||||||||||||||
![]()
|
Définition |
Nombre dont la somme des diviseurs non triviaux est égale
à la somme des carrés de ses chiffres. |
|
Exemple |
Div(125) = {1, 5, 25, 125} DivNon-triviaux (125) = {5, 25} =>
somme 5 + 25 = 30 Somme des carrés des chiffres: 1² + 2² + 5² = 30 |
|
Voir |
|
|
|
|
|
Nombres canadiens parfaits Ils sont quatre seulement: 125, 581, 8 549 et 16 999. 125, {1,
5, 25, 125} => 5 + 25 = 30 et 1² + 2² + 5² =
30 581, {1,
7, 83, 581} 8 549, {1,
83, 103, 8549} 16 999, {1, 89, 191, 16999} Avec les cubes (jusqu'à 100 000) 142,
{1, 2, 71, 142} => 2 + 71 = 73 et 13
+ 43 + 23 = 73 160,
{1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80, 160} 1 375,
{1, 5, 11, 25, 55, 125, 275, 1375} 6 127, {1,
11, 557, 6127} 12 643, {1, 47, 269, 12643} 51 703, {1, 149, 347, 51703} 86833, {1, 71, 1223, 86833} Avec les puissances 4 (jusqu'à 100 000) 1 005, {1,
3, 5, 15, 67, 201, 335, 1005}} =>
3+5+15+67+201+335 = 626 = 14 + 54 5 405, {1,
5, 23, 47, 115, 235, 1081, 5405} 89 195, {1, 5, 17839, 89195} 92 029, {1, 7, 13147, 92029} Avec les puissances 5 (jusqu'à 100 000) Aucun |
|
|
|
||
|
|
Commentaires Ouverture des logiciels de théorie des nombres. Lancement d'une boucle d'exploration des nombres
n de 1 à 1000. Obtention de la liste des chiffres de n dans N
(via une conversion en base 10). Addition des carrés des chiffres dans C. Liste des diviseurs de n dans E. Somme des diviseurs sauf le premier et le denier
dans F. Si la somme des diviseurs est égale à la somme
des carrés, imprimer le nombre et ses diviseurs. En bleu, résultat de l'exécution du programme. |
|
Voir Programmation – Index
![]()
|
Site |
OEIS A070308 – Canada perfect numbers: n such that the sum of
digits^2 of n equals the sum of d|n, 1<d<n. |
|
Livre |
Ces nombres qui nous fascinent – J.-M. De Koninck |
|
Cette page |
![]()