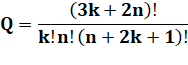Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 03/06/2025 M'écrire Brèves de Maths

INDEX Graphe Logique Suites pour dénombrer Dénombrement Jeux et énigmes	Dénombrements - MOTIFS
	Nombres de Catalan		Nombres de Naryana		Nombres Manhattan
	Nombres de Catalan – Développements
	Définition	Pascal		Parenthèses		Polygones
	Valeurs	Hipparque		Escaliers		Illustrations
	Fuss-Catalan	Chemins de Dyck		Arbres

Faites un double-clic pour un retour en haut de page

Eugène Catalan	Nombres de Catalan	Constante de Catalan	Conjecture de Catalan
	Hyper-Catalan	Résolution des équations

NOMBRES HYPER-CATALAN Les nombres de Catalan dénombrent, entre autres, les triangles dans les polygones. Les nombres hyper-Catalan dénombrent tout type de polygones dans les polygones. En 2025, les mathématiciens inventent une méthode de résolution des équations de degré quelconque en utilisant ces nombres. Les solutions se présentent sous la forme de séries.
	Sommaire de cette page >>> Nombres Hyper-Catalan >>> Tableau des nombres Hyper-Catalan bi-tri	Débutants Dénombrement Glossaire Combinatoire

Anglais : Hyper-Catalan Numbers

Nombres Hyper-Catalan		haut
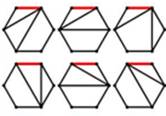
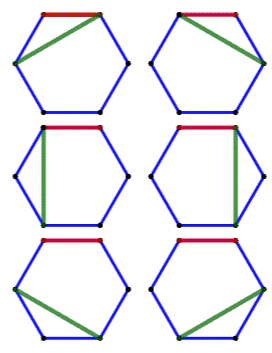
Nombre hyper-Catalan Généralisation des nombres de Catalan servant à compter les triangles dans les polygones. Combien de polygones de variétés données compte-t-on dans un polygone partagé par des diagonales non-sécantes ? Exemple de dénombrement avec l'hexagone Pour éviter les permutations et les rotations, on maintient le côté rouge de l'hexagone en haut (trait rouge). Le but est de partager l'hexagone en pentagones et en triangles. La figure montre les six possibilités. Il a six (6) solutions avec des triangles (t2) et des pentagones (t4). Numérotation avec le nombre de côtés moins 1. Soit la notation complète: 6 t2 t4	Hexagone divisé en triangles et pentagones
Définition en bref Les nombres hyper-Catalan sont une généralisation des nombres de Catalan, une séquence combinatoire qui indique comment découper un polygone en triangles, en carrés, en polygones, y compris leur panachage.	Un nombre hyper-Catalan bi-tri dénombre les divisions des polygones en triangles et en carrés

Tableau des nombres Hyper-Catalan bi-tri			haut
Ces nombres sont utilisés pour la résolution des équations de degré quelconque, y compris supérieur à 4.
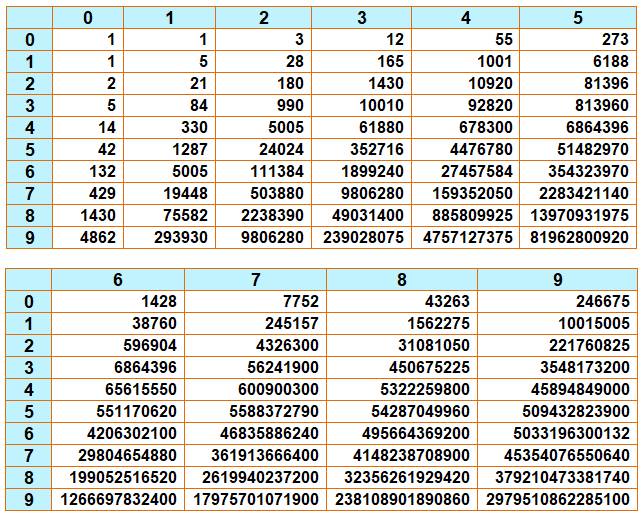
Tableau avec k en ligne et n en colonne La colonne 0 est celle des nombres de Catalan. La ligne 0 est celle des nombres de Fuss.
Propriété Utilisée pour la résolution des équations avec des séries.	La somme alternée sur les diagonales montantes est égale à 0. 2 – 5 + 3 = 0 5 – 21 + 28 – 12 = 0 14 – 84 + 180 – 165 + 55 = 0 etc.

Suite	Arbres en général – Introduction, types Catalan et parenthèses Catalan et triangle de Pascal Historique des suites de nombres pour compter Nombres de Motzkin Nombres de Genocchi
Voir	Billard Coefficient du binôme Conjecture de Catalan Constante de Catalan Dénombrer – Index Eugène Catalan	Factorielle Méandres Nombres de Bell Premier Sous-factorielles
Sites	OEIS A104978 - Triangle read by rows, where the g.f. satisfies A(x, y) = 1 + x*A(x, y)^2 + x*y*A(x, y)^3 OEIS A000108 – Catalan numbers OEIS A001764 – Fuss numbers A Hyper-Catalan Series Solution to Polynomial – Equations, and the Geode – N. J. Wildberger & Dean Rubine – pdf 21 pages Paper with Dean Rubine on solving polynomial equations – Vidéo
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDENOM/Catalan/Hyper.htm