Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 22/11/2024 M'écrire Brèves de Maths

INDEX Narcissiques Somme-Produit Ch Formes et motifs Nombres en chiffres Chiffres Sommes de nombres Types de nombres Jeux et énigmes	Types de Nombres – Sommes
	Smith	Jonction	Auto-nombre	Docile
	Étonnants	Obstinés

Faites un double-clic pour un retour en haut de page

NOMBRES obstinés, détendus et souples Nombres sommes d'un nombre impair et d'une puissance de 2.
	Sommaire de cette page >>> Le	Débutants Nombres Glossaire Nombres

Nombres obstinés			haut
Obstiné ou souple Un nombre obstiné est un nombre impair qui n'est pas somme d'un nombre premier et d'une puissance de 2. Sinon, il est souple. Notez que si k = 1 et N est premier, nous sommes en présence de nombres premiers jumeaux.		Nombre obstiné
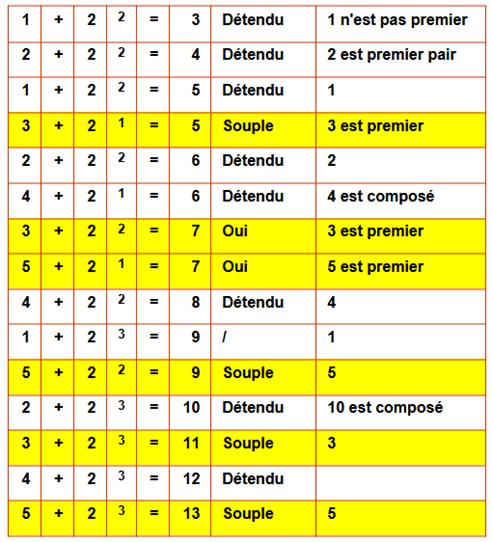
Exemples	Le nombre 5, impair, n'est pas obstiné : 5 = 3 + 2 ; il est SOUPLE. Le nombre 7, impair, n'est doublement pas obstiné : 7 = 5 + 2 = 3 + 2² ; il est SOUPLE. Le nombre 905 est le nombre OBSTINÉ le plus petit. Le nombre 4, pair est bien égal à 2 + 2, il ni obstiné, ni souple, il est DÉTENDU.

Liste		haut
Nombres de 3 à 13
Liste des nombres obstinés	1, 3, 127, 149, 251, 331, 337, 373, 509, 599, 701, 757, 809, 877, 905, 907, 959, 977, 997, 1019, 1087, 1199, 1207, 1211, 1243, 1259, 1271, 1477, 1529, 1541, 1549, 1589, 1597, 1619, 1649, 1657, 1719, 1759, 1777, 1783, 1807, 1829, 1859, 1867, 1927, 1969, 1973, …
Liste des nombres obstinés composés	905 = 5 x 181 905, 959, 1199, 1207, 1211, 1243, 1271, 1477, 1529, 1541, 1589, 1649, 1719, 1807, 1829, 1969, 1985, 2171, ...

Programmation		haut
Programme Maxima	But Produire la liste des nombres obstinés composés. Commentaires Reset pour initialiser le programme. Déclaration d'une liste S. Double boucle pour n et k et calcul de p = n + 2^k. Limitation des sorties à moins de 5000. Test si n est premier. Si Oui, introduction de p dans la liste S. Transformation de la liste en ensemble (T) pour éliminer les doublons. Création de la liste des entiers impairs en en L, puis mise sous forme d'un ensemble. Différence entre les entiers et les nombres obstinés trouvé en D. Boucle d'élimination des nombres premiers dans la liste des obstinés. Et impression de ceux-ci. Exemple de sortie de 905 à 1243

Haut de page (ou double-clic)

Suite	Nombres jonctions Nombres de Smith Auto-nombres Somme-Produit des chiffres – Index
Voir	Nombres de 1 à 100 et leurs diviseurs Nombre -motif de Smith Grand nombre de Smith Nombre Diviseurs Additifs
Sites	OEIS A133122 – Odd numbers which cannot be written as the sum of an odd prime and 2^i with i > 0.
Cette page	http://villemin.gerard.free.fr/aNombre/TYPADD/Obstine.htm