NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 15/12/2015

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique                               

     

Nombres

 

Débutants

Général

ÉTUDES

 

Glossaire

Général

 

 

INDEX

Nombres

Nombre 36

Nombre 70

Nombre 81

Nombre 999

 

Sommaire de cette page

>>> Approche

>>> Le plus grand

>>> Propriétés

>>> Affirmation à propos de 70

>>> Nombres 21 à 40 et leurs copremiers

 

 

 

 

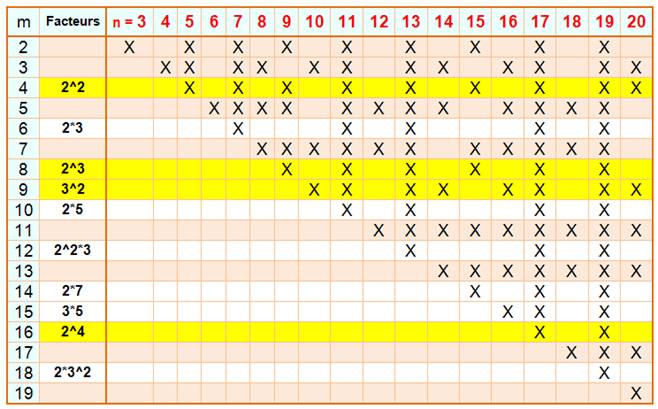
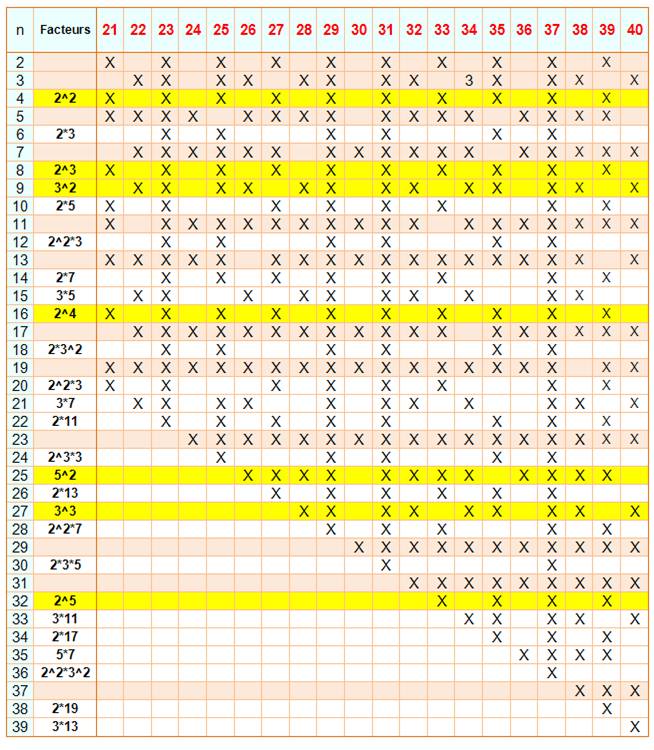
Nombres 70 et autres …

et leurs copremiers

 

Copremiers de n: ce sont tous les nombres m inférieurs à n et premiers avec n.

Le nombre 70 résulte d'une affirmation qui s'est avérée fausse et que nous analysons dans cette page.

Le nombre 60 est le plus grand nombre à copremiers sans facteur simple.

 

 

APPROCHE

 

*  Cherchons quels sont les copremiers m des nombres n.

*  Identifions les copremiers m qui sont premiers (marron) et ceux qui sont composés à facteurs à une puissance quelconque jaune)

*  Les lignes blanches montrent les copremiers m qui comporte un facteur simple (sans puissance)

 

 

*  Nous constatons que n = 3, 4, et 5 ont des copremiers premiers ou avec puissances (lignes colorées).

*  Et que le nombre 7 est le premier qui soit copremier avec n nombre comportant au moins un facteur simple: 6 = 2 x 3 (noté dans le tableau 2*3 pour éviter la confusion avec la lettre x).

 

 

 

 

Le plus grand NCSFS

 

*  Nommons les nombres 3, 4, 5 des NCSFS (nombre avec copremiers sans facteurs simples).

*  Le tableau montre quelques tels nombres:

 

2, 3, 4, 5, 6, 8, 10, 12, 14, 18, 20

 

*  Quels sont les suivants? Sont-ils nombreux?

Voici les suivants:

 

24, 30, 42, 60.

 

*  Ils sont seize en tout et pour tout et le plus grand est 60.
Ce sont des nombres qui possèdent une grande quantité de diviseurs.

 

 

 

Affirmation erronée

70 => {3, 9, 11, 13, 17, 19 … 69}

*  Les nombres copremiers avec 70 seraient tous

*    premiers ou

*    puissance de premier.

Et, le nombre 70 serait le plus grand nombre ayant cette propriété.

*  Affirmation fausse prêtée à Erdös.
Le plus grand étant 60.

*  Comparaison entre les nombres 60 et 70 et tous leurs copremiers:

 

 

Nombres 21 à 40 et leurs copremiers

 

 

 

 

 

 

Retour

*       Nombre 70

*       Nombre 60

Suite

*       Nombres premiers entre eux

*       Nombres premiers – Index

Voir

*       Divisibilité par N

*       Énigme et puzzles – Index

*       Nombres – Nomenclature

*       TABLES – Index

Cette page

*       http://villemin.gerard.free.fr/aNombre/Nb0a1000/Nb70.htm