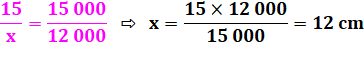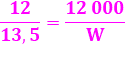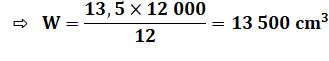le bassin, géométrie en cm2

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/11/2017 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	MATHS en PRIMAIRE
Débutants Général	Géométrie		Glossaire Général
INDEX Géométrie Arithmétique et Algèbre Enseignement	Initiation	Exercices	Bassin
	CM2	Sommaire de cette page >>> Problème de bassin

Exercices typiques de géométrie

Bassin et niveaux d'eau

Un problème typique de calcul de niveaux d'eau dans un bassin parallélépipédique (pavé droit). Il a même des fuites …

Résolution pas à pas avec un bon dessin pour représenter les situations.

Problème de bassin

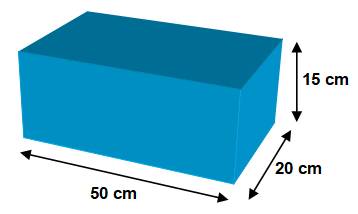
Un bassin en forme de pavé droit de 50 cm x 20 cm et 15 cm de hauteur. Il est rempli d'eau à ras bord.

Je visualise le bassin en forme de pavé (parallélépipède). Le fond mesure 50 cm de long et 20 cm de large. Il est haut de 15 cm.

Question 1)

Quel est le volume d'eau dans le bassin?

Je me souviens qu'un volume, c'est la multiplication de trois dimensions (3D). Il se mesure en m³ ou en cm³ (comme ici).

Pour un pavé droit, c'est:

V = longueur x largeurs x hauteur.

V = 50 x 20 x 15 = 15 000 cm³

J'apprécie ce volume.

C'est beaucoup moins d'un mètre cube, car toutes les dimensions sont inférieures à 1 m.

C'est plus qu'un litre car les dimensions sont supérieures à 10 cm (1litre = 10 cm x 10c m x 10 cm = 1000 cm³).

V = 15 dcm³ = 15 litres.

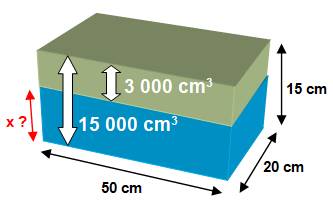
Question 2)

On vide 3 000 cm³. Quel est le nouveau niveau dans le bassin?

Seule varie la hauteur d'eau.

Pour 15 cm, le volume est 15 000 cm³

Pour quelle hauteur x nous aurons un volume de 15 000 – 3000 = 12 000 cm³?

C'est un problème de proportions. Je cherche la quatrième proportionnelle (produit en croix):

Question 3)

On ajoute de l'eau pour atteindre une hauteur de 13,5 cm. Quel est le volume d'eau ajouté?

Niveau actuel:

12 cm pour 12 000 cm³

Nouveau niveau à atteindre:

13,5 cm pour un volume inconnu W.

Calcul de W (Quatrième proportionnelle):

Volume d'eau ajouté:

Va = 13 500 – 12 000 = 1 500 cm³

Question 4)

Le bassin fuit à raison de 50 ml par heure. Combien de temps pour que le bassin soit vide?

Je me souviens que 1 cm³ = 1 ml. Pour cela, je vérifie que 1000 cm³ = 1 litre: en gros, mille petit cubes de la taille de mon pouce, ça remplit bien une bouteille.

Volume d'eau actuel: 13 500 cm³ = 13 500 ml.

Durée d'écoulement: 13 500 / 50 = 270 heures.

Quantité de jours: 270 / 24 = 11,25 jours.

Et 0,25 jour (1/4 de jour) = 6 heures.

Soit: en 11 jours 6 heures le bassin sera vide.

Suite	Problèmes de logique (CM2)
Voir	Calculs – Juniors – Index La méthode de Singapour Calculs qui affolent le Net
Magazine et site	Maths – La méthode de Singapour – Le point – Novembre 2017
Cette page	http://villemin.gerard.free.fr/aMaths/Primaire/Geometri/Bassin.htm