|
||||||||||||||||||||||||||||||||||||
![]()
|
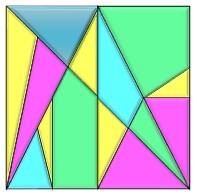
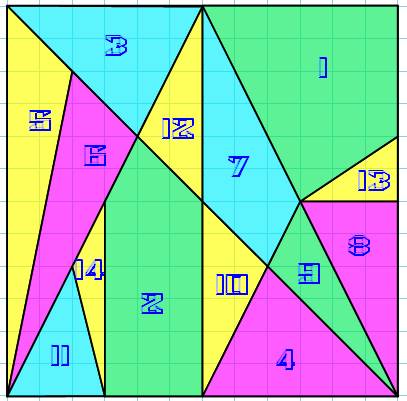
Loculus d'Archimède Stomachion (de Suter)
Archimède (287 av. J.-C. - 212 av. J.-C.)
décrit ce puzzle dans le palimpseste
d'Archimède. Sans doute le plus vieux puzzle connu. Jeu de découpage façon Tangram. |
Anglais: loculus of Archimedes, Archimedes' box, syntemachion,
stomachion, ostomachion
A put-together puzzle / Tiling the square
|
|
||
|
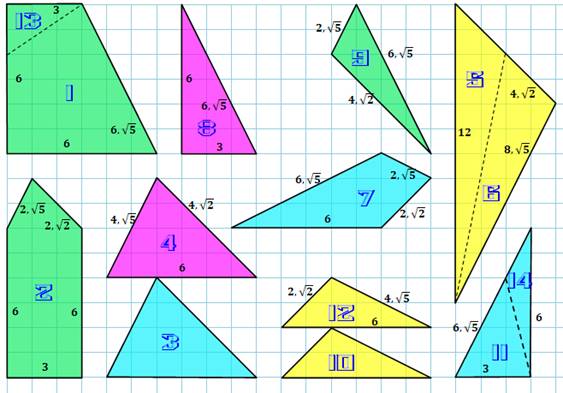
En chiffres Carré de 12 x 12 14 pièces dont deux non-triangulaires et deux
d'entre elles sont dupliquées. 17 152 façons d'assembler les pièces en un carré.
536 en éliminant les rotations et réflexions.
Calculé par Bill Cutler et indépendamment par d'autres mathématiciens: Persi
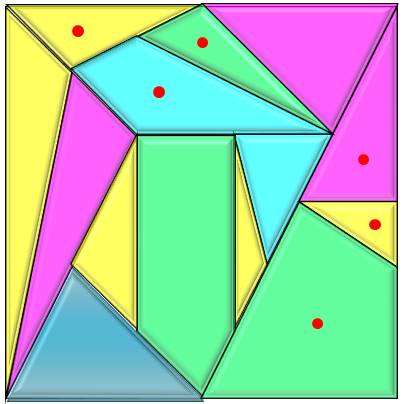
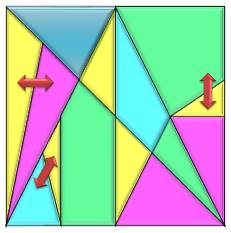
Diaconis, Susan Holmes, Ronald Graham et Fan Chung. Les pièces peuvent être posées recto ou verso. Si
elles sont toutes recto sur l'exemple du haut, alors six sont verso sur
l'exemple du bas (points rouges). Comme le Tangram, les pièces peuvent être
assemblées en diverses figures. Nom Stomachion est un diminutif d'Ostomachion qui
signifie lutte, combat d'os, car joué avec des pièces en os ou en ivoire. Historique Connu d'Archimède et de bien d'autres Grecs. Ce n'était pas un jeu, mais une dissection du
carré en 14 pièces avec la contrainte que l'aire de chaque pièce soit une
proportion rationnelle (une fraction exacte) de l'aire du grand carré. Heinrich
Suter (1848-1922) est un historien des sciences spécialisé en
mathématiques et astronomie islamique. Il proposait le nom de syntemachion. |
|
|
|
|
||
|
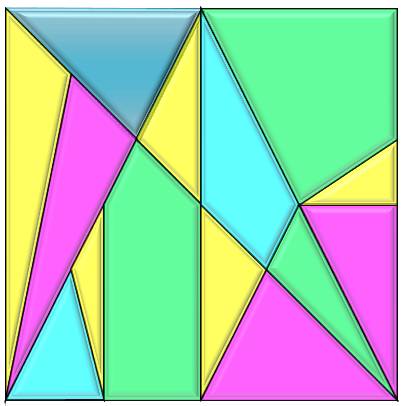
Construction Pour obtenir les pièces de ce puzzle:
Ensuite :
Avec une feuille quadrillée, c'est plus facile. Propriété Toutes les pièces ont été choisies avec des
sommets sur le quadrillage du carré 12
x 12. Bien! C'est facile ! Mais les aires de toutes ces pièces sont des
nombres entiers. Bravo ! C'est astucieux et pas banal. |
Les aires et les coordonnées des sommets sont des nombres rationnels. Pas toutes les
longueurs des côtés. |
|
|
|
||
|
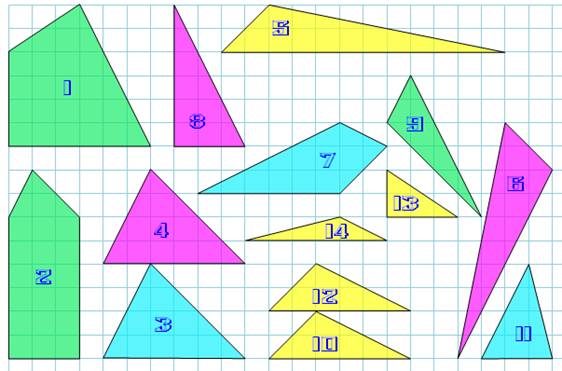
Formes Deux paires isométriques: 3 = 4 10 = 12 Deux non triangulaires: 1 et 2 Ce sont les deux plus grandes. Deux triangles avec trois longueurs irrationnelles: 6 et 9 Les autres triangles ont au moins une longueur rationnelle (nombre
entier sur la grille pour les côtés horizontaux sur la figure du bas) |
|
|
|
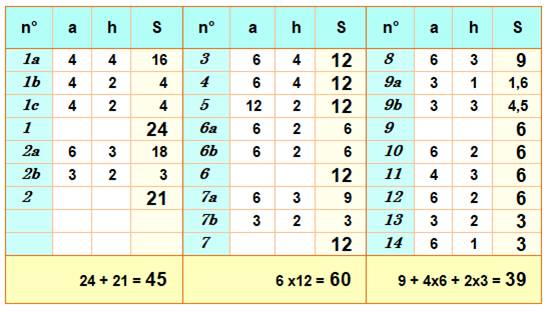
Aires Aire totale: 144 Les pièces non-simples sont découpées en triangles rectangles, carrés
ou rectangles, comme 1a + 1b + 1c = 1 |
|
|
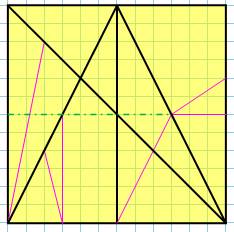
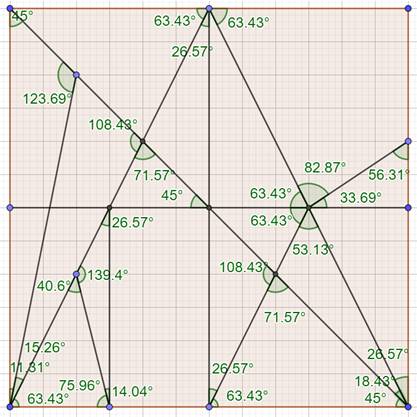
Angles Exemple de calcul Le premier angle en bas à gauche correspond à: tan (A) =
2/10 = 0,2 arctan(0,2) = 11,31° Un autre en haut: tan(A) = 4/2 = 2 arctan(2) = 63,43° La figure montre
les angles calculés avec GeoGebra. |
|
|
|
||
|
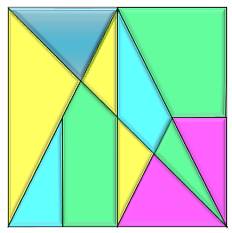
Trois paires de pièces sont toujours ensembles et dans la même
position pour toutes les solutions. De sorte que le puzzle pourrait se limiter à 11 pièces (figure de
droite). |
|
|
|
|
||
|
Notre question Quelle
est la probabilité d'obtenir un triangle
à aire rationnelle en choisissant les sommets sur une grille 4 x4
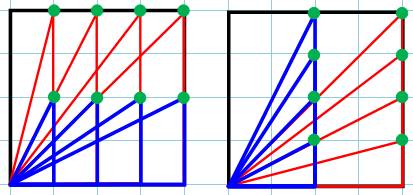
(par exemple) ? Cas des triangles rectangles En partant du sommet en bas à gauche, il suffit de positionner l'autre
sommet sur un des points verts. Ils se trouvent sur une ligne ou une colonne
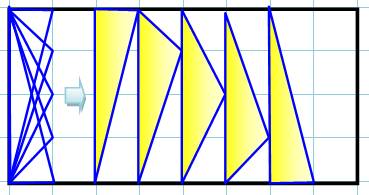
paire. Cas des triangles non-rectangles Le choix du sommet peut se faire n'importe où sur la colonne, l'aire
du triangle reste constante (demi produit de la base par la hauteur). Même chose pour les hauteurs plus importantes. Conclusion Sans minimiser la trouvaille des Anciens, la probabilité de
sélectionner des triangles rationnels est assez grande. Encore faut-il
trouver une combinaison astucieuse ! |
L'aire de chacun de ces triangles est rationnelle. Le produit des
(mesures des) deux côtés de l'angle droit est divisible par 2.
Tous ces triangles, avec la même base et la même hauteur, ont la même aire rationnelle
(= 4x1/2 = 2). |
|
|
|
||||
|
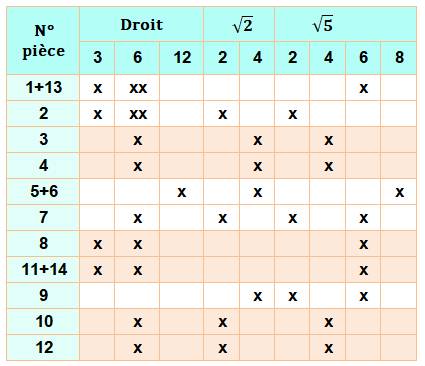
Identification des pièces Il existe 9 types de côtés pour ces 11 pièces (jumelages
faits). Il y a 8 types de pièces en regroupant les 3 doublons (3,4; 10,12;
8,11). On note la longueur des côtés en unités de grille pour les côtes
horizontaux ou verticaux, ou en longueur oblique avec la pente pour les
autres côtés. Ainsi (6, rac5) veut dire que la longueur oblique vaut 6 et la pente
vaut racine de 5. |
|
|||
|
Types de pièces selon côtés Le tableau montre quels sont les types de côtés pour chaque pièce de 1
à 14. C'est avec ce type de recensement que l'on peut associer les pièces selon
leur longueur (ou un multiple) et la
nature de la pente. Il est possible d'établir un graphe
des possibilités d'assemblage et d'en déduire des règles pour reconstituer le
carré complet. |
|
|||
|
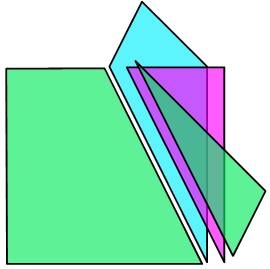
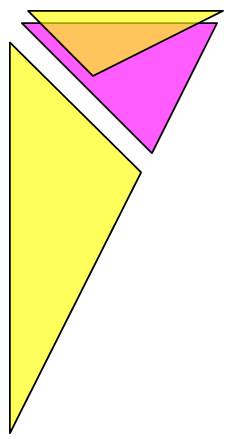
Exemples de possibilités d'assemblage |
|
|||
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()