|
||||||||||||||||||||||||||||
![]()
|
Une énigme géométrique de calcul d'aires.
Deux solutions possibles: le calcul classique ou, plus astucieusement, un
raisonnement géométrique façon Tangram
(par déplacement des figures élémentaires. Cerise sur le gâteau: une
démonstration muette … |
|
|
|
|
Dans
le rectangle matérialisé en bleu, comparez la surface de la zone couverte par
le sapin à celle de la zone blanche qui l'entoure.
Indice: Le calcul
pourquoi pas, mais existe-t-il une solution évitant de trop nombreux calculs?
La zone de recouvrement me semble préoccupante. Réfléchissons … |
|
Voir Solution
|
|
|||
|
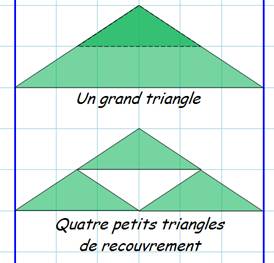
Zone de
recouvrement Chaque petit triangle
de recouvrement est semblable au grand triangle
du fait que leurs bases sont parallèles. Nous constatons sans problème que
les hauteurs sont dans le rapport ½. C'est la même chose pour les bases (Théorème de Thalès). Les aires sont dans le rapport 1/4.
Dit-autrement: les quatre petits triangles de recouvrement ont une aire égale
à celle du grand triangle. |
L'aire
du grand triangle est égale à celle des quatre petits triangles de
recouvrement. |
||
|
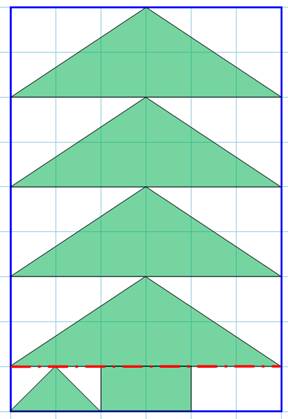
Élimination du
recouvrement De cette première constatation,
nous en déduisons que les cinq grands triangles occupent la place de 5 – 1 =
4 grands triangles. Sans recouvrement les cinq triangles occuperaient 5
Trg. Ils se recouvrent sur une surface équivalente à un des triangles.
Laquelle est donc à retrancher. Ce qui donne 5 – 1 = 4 Trg Nous voilà avec des surfaces
propres (sans recouvrement):
Nous en profitons pour les
repositionner astucieusement. |
|||
|
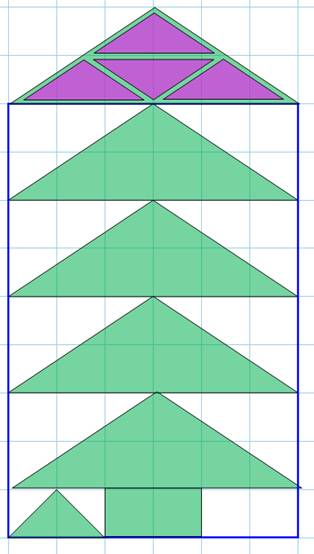
Recomposition
du dessin Dans la zone des quatre grands
triangles (en haut du trait pointillé
rouge), la zone verte est équivalente en surface à la zone blanche. Chaque triangle vert occupe la moitié de l'espace. Dans la zone du bas, le
rectangle vert compense le même rectangle en blanc; Quant au triangle à gauche, sa
zone verte est équivalente à la zone blanche. |
|
||
|
Conclusion Le sapin en vert occupe la même
surface que la zone en blanc qui
l'entoure. |
|||
Retour Énoncé / Voir la démonstration
muette
|
|
||
|
|
||
|
|
T = ½ x 6 x 2 = 6 |
|
|
|
Tr = ½ x 3 x 1 = 1,5 |
|
|
|
T5 = 5 x 6 – 4 x 1,5 = 30 –
6 = 24 |
|
|
|
R = 2 x 1 = 2 |
|
|
|
Ts = ½ x 2 x 1 = 1 |
|
|
|
Av = 24 + 2 + 1 = 27 |
|
|
|
Ar = 6 x 9 = 54 |
|
|
|
R = Av / Ar = 27 / 54 = 1/2 |
|
|
La zone verte occupe autant
de place que la zone blanche. |
||
|
|
||
|
1) Placez le chapeau en bas; 2) Faites glisser les grands
triangles vers le haut pour éliminer le recouvrement; 3) Placez les quatre zones de
recouvrement sur le triangle du haut, celui qui dépasse et qui, de ce fait
sera éliminé; et 4) Conclusion: dans le rectangle
bleu, zone verte et zone blanche sont équivalentes en surface. |
||
|
|
|
|
![]()
![]()