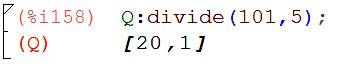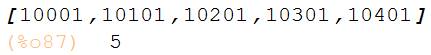|
|||||||||||||||||||||||||||||||||||||
![]()
|
MAXIMA & les
CHIFFRES Programmation Programme d’extraction des chiffres d’un nombre
et applications. |
|
Programmes de familiarisation avec Maxima |
|
|
|
Mon premier
programme
|
Comment
trouver les chiffres du nombre 45 et les exprimer sous forme d’une
liste? |
|
|
Division
|
L’instruction
division réalise la division
euclidienne dont la sortie est la liste donnant le quotient suivi du
reste. |
|
|
Fonction
extraction des unités
Optimisation
|
On
commence par s’exercer avec une fonction qui fournit les dizaines et les
unités d’un nombre. Les
unités sont le reste de la division par 10 d’un nombre, soit : u = n mod
10. Les
dizaines sont obtenues en retirant les unités et en divisant par 10. On
retourne la liste de ces deux nombres. 1)
L’instruction division donne directement la liste
quotient et reste. 2)
L’instruction block peut être omise. Son rôle
consiste à isoler des variables utilisées localement. 3)
Par défaut, le retour de la fonction est le
dernier calcul. |
|
|
Extraction des
chiffres
|
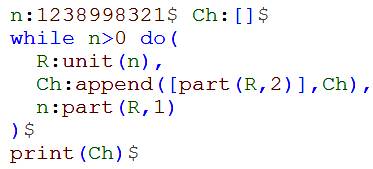
On
se donne un nombre n dont on veut extraire les chiffres dans une liste Ch. Tant
que n reste positif, on itère les instructions suivantes :
|
|
|
|
||
|
Fonction
extraction des chiffres
|
Commentaires Utilisation
d’un block avec variables locales :
Ch, la liste des chiffres et R, la liste quotient, reste de la division. Le calcul est exactement le même que celui
exposé ci-dessus. La
liste des chiffres Ch est retournée (return). |
|
|
Fonction
conversion en base b
|
Commentaires Programme
qui convertit un nombre décimal en liste des chiffres de ce nombre en base b. L’instruction
division est modifiée en conséquence. Le
premier exemple exprime 1024 = 210 en binaire, un 1 suivi de dix
0. Le
second donne un exemple en base 12. En effet, 150 = 144 + 6 = 122
+ 6. |
|
|
Extraction des
chiffres et conversion - Autre version
|
Une autre version vue sur Internet (Rosetta Code). Même
principe que ci-dessus, avec la nuance que la base 10 est implicite. L’argument
nb est mis sous forme de liste dont la longueur (length) détermine la
suite :
Dans
tous les cas, le nombre n à convertir est pris comme le premier élément
(first) de l’argument. |
|
Voir Racines numériques additives
et multiplicatives
|
|
||
|
Recherche de
palindrome
|
La
fonction palindrome utilise la fonction recherche des chiffres vue ci-dessus. Il
s’agit de vérifier la symétrie des chiffres. Pour cela, on fait l’hypothèse que
le nombre est palindrome (T=1) et si un seul test de symétrie est défaillant,
ce témoin est mis à 0. |
|
|
Liste de
nombres palindromes
|
Ce
programme liste les nombres palindromes dans L. Si
le retour de la fonction Palin est à 1, le nombre est retenu et ajouté à la
liste L (append). On
imprime la liste et sa longueur. |
|
|
|
||
|
|
La
recherche des carrés ayant deux chiffres identiques utilise la fonction
Chiffre vue ci-dessus. Une
première boucle explore les nombres n ; une seconde explore les chiffres
de chaque nombre. Si
les chiffres de rang i et i+1 sont égaux, on imprime le nombre et son carré. On
maitrise bien les symboles
|
|
|
|
||
|
|
Il
s’agit ici de sélectionner les nombres ayant tous ses chiffres différents et
uniques. Avec
la fonction chiffre vue ci-dessus, on forme la liste C des chiffres de n. L’instruction
setify (passer à un ensemble) transforme
la liste c en un ensemble D, lequel élimine les doublons des chiffres. Il
suffit de comparer la taille (length) des deux ensembles. S’i elles sont égales,
alors tous les chiffres sont différents.
|
|
|
Programme wxMaxima
2020" "501" "1012020" " 2021" "10001" "20212021" " 2022" "5001" "10112022" " 2023" "10001" "20232023" " 2024" "1251" "2532024" " 2025" "401" "812025" " 2026" "5001" "10132026" " 2027" "10001" "20272027" " 2028" "2501" "5072028" " 2029" "10001" "20292029" " 2030" "1001" "2032030" "
|
But Produire le plus petit coefficient k Commentaires Pour un débutant, le principal souci consiste à placer les
ponctuations. Dans la boucle for, les instructions se suivent séparées par une virgule. La dernière instruction est suivie de la fermeture de la parenthèse. La boucle se termine par ; si on veut une impression ou (comme ici) par $ pour éviter l’impression. Dans la boucle while, même chose : des virgules dans les parenthèses sauf pour la dernière instruction, et une virgule derrière la parenthèse, car nous sommes à l'intérieur de la boucle for. L'incrémentation k:k+1 n'est pas suivi de ponctuation car la dernière instruction de la boucle while. La parenthèse qui suit est vierge car dernière instruction de la boucle for. La parenthèse finale est suivi de $ comme nous l'avons dit plus haut, c'est la fermeture de la boucle for. |
|
![]()
|
Retour |
|
|
Suite |
|
|
Sites |
|
|
Cette page |
![]()