|
Édition du: 31/07/2025 |
Faites
un double-clic pour un retour en haut de
page
![]()
|
PROGRAMMATION PYTHON – GRAPHES avec PLOT Mes premiers pas avec
matplotlib. Le minimum nécessaire à savoir pour visualiser une fonction. Les tutoriels
sur Internet vous permettront de raffiner vos présentations. Notez que GeoGebra est aussi un excellent outil simple pour
visualiser le graphe d'une fonction. |
||
|
|
Sommaire de cette page >>>
Graphes de points >>>
Dessin d'une courbe >>>
Graphe de fonction 1 >>>
Graphe de fonction 2 |
Débutants Glossaire |
Voir absolument Mon espace de travail en
Python
Voir Comment installer
les extensions comme matplotlib
|
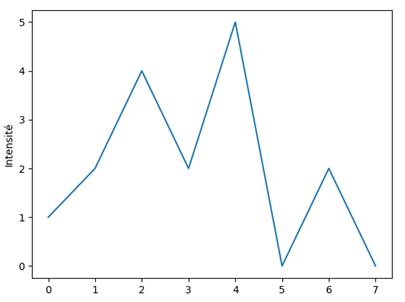
Graphe de points simple (X implicite)
|
import matplotlib.pyplot as plt plt.plot([1, 2, 4, 2, 5, 0, 2, 0]) plt.ylabel('Intensité') plt.show()
|
|
|
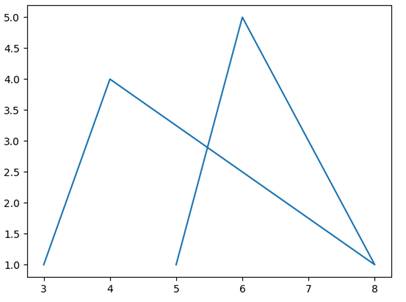
Graphe de points en X, Y
|
import matplotlib.pyplot as plt fig, ax = plt.subplots() ax.plot([3, 4, 8, 6, 5], [1, 4, 1, 5, 1]) plt.show()
|
|
|
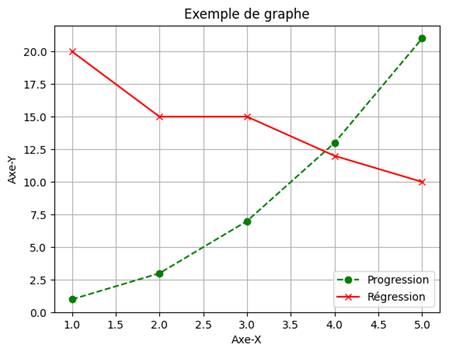
Graphe complet: points et lignes
|
import matplotlib.pyplot as plt x = [1, 2, 3, 4, 5] y1 = [1, 3, 7, 13, 21] y2 = [20, 15, 15, 12, 10] plt.plot(x, y1, label='Progression', color='green', linestyle='--', marker='o') plt.plot(x, y2, label='Régression', color='red', linestyle='-', marker='x') plt.grid(True) plt.xlabel('Axe-X') plt.ylabel('Axe-Y') plt.title('Exemple de graphe') plt.legend() plt.show()
|
|
|
numpy.linspace(0, 10, 100) |
Renvoie
100 points régulièrement répartis entre 0 et 10. La quantité de points est égale à 50 par défaut. |
Suite en: numpy.linspace
|
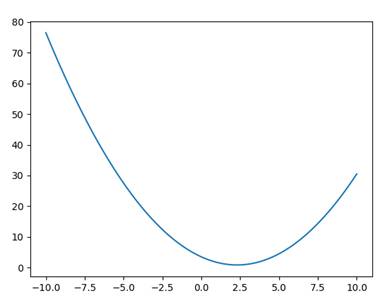
Graphe de points simple (X implicite)
|
import matplotlib.pyplot as plt import numpy as np x = np.linspace(-10, 10, 100) y = 0.5*x**2 - 2.3*x + 3.5 plt.plot(x, y) plt.show()
|
|
|
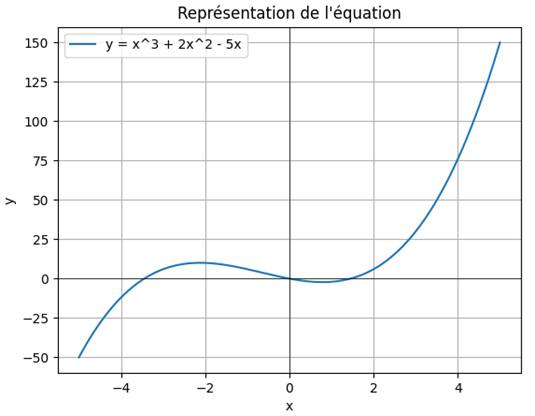
Avec définition d'une fonction en y Nécessité de sympy pour avoir accès aux symboles. Fonction écrite en clair en fonction de x. Créations de 400 échantillons avec linspace. Puis, toutes les commandes de tracé du graphe. |
from sympy import symbols import numpy as np import matplotlib.pyplot as plt # Définir la variable x x = symbols('x') # Définir la fonction def f(x): return x**3 + 2*x**2 - 5*x # Créer un intervalle de valeurs X = np.linspace(-5, 5, 400) Y = f(X) # Tracer le graphe plt.plot(X, Y, label='y = x^3 + 2x^2 - 5x') plt.axhline(0, color='black', linewidth=0.5) plt.axvline(0, color='black', linewidth=0.5) plt.grid(True) plt.legend() plt.title("Représentation de l'équation") plt.xlabel("x") plt.ylabel("y") plt.show()
|
|
|
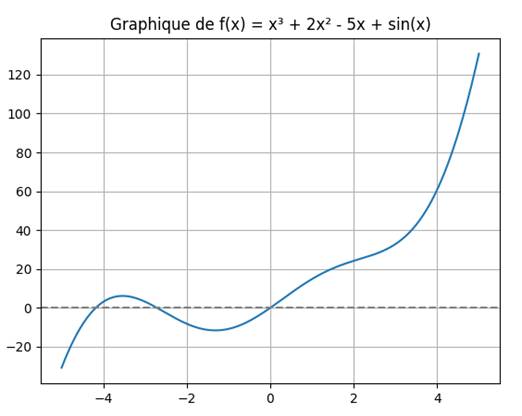
Avec une référence horizontale Spécification directe de la fonction en reprenant bien la notation de
X en majuscule. Puis, toutes les commandes de tracé du graphe. A titre illustratif, introduction d'une composante trigonométrique
dans la fonction |
import matplotlib.pyplot as plt import numpy as np X = np.linspace(-5, 5, 400) Y = X**3 + 2*X**2 - 5*X + 20*np.sin(X) plt.plot(X, Y) plt.axhline(0, color='gray', linestyle='--') plt.title("Graphique de f(x) = x³ + 2x² - 5x + sin(x)") plt.grid() plt.show()
|
|
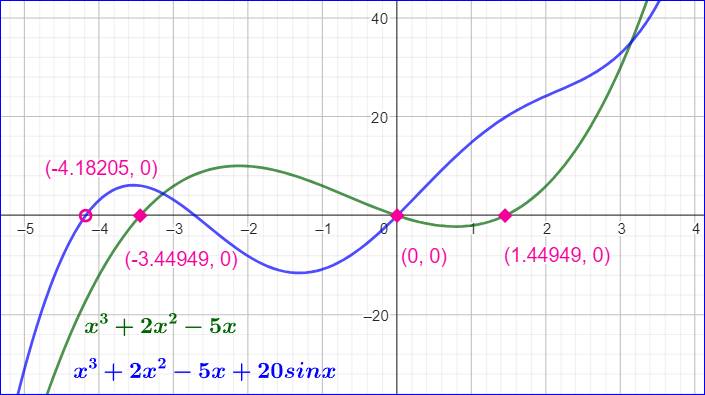
Pour
information: les graphes créés par GeoGebgra
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()