|
Édition du: 29/07/2025 |
|
INDEX |
Python –
Comment se lancer et initiation |
||
Faites un double-clic pour un retour en haut de page
![]()
|
PYTHON: Trucs et astuces Combinatoire Quelles sont les
principales choses à savoir ou à avoir sous la main lorsqu'on s'intéresse aux
dénombrements,
combinaisons,
permutations,
arrangements. |
||
|
|
Sommaire de cette page >>>
Combinaisons >>>
Permutations >>>
Permutations et combinaisons – Comparaison >>>
Anagrammes numériques >>>
Exemple avec affichage d'une table |
Débutants Glossaire |
|
Combinaisons de 3 parmi 4 Chaque combinaison (comb) est un tuple (1, 2, 4) L'instruction avec join, assemble
les éléments d’une séquence en les séparant par le texte entre parenthèses. |
from itertools import combinations A = [1, 2, 3, 4] C = list(combinations(A, 3)) for comb in C:
print("-".join(str(x)\ for x in comb)) |
1-2-3 1-2-4 1-3-4 2-3-4 |
|
|
Toutes les combinaisons Note: Voyez comment imprimer les objets sans
l'apostrophe avec join (conversion des éléments en une chaîne formatée). |
from itertools import combinations L = ['a', 'b', 'c', 'd'] C = [] # Combinaisons de longueur 1 à 4 for r in range(1, len(L) + 1): CC = list(combinations(L, r)) C.extend(CC) # Affichage for comb in C: print(",".join(comb)) |
a b c d a,b a,c a,d b,c b,d c,d a,b,c a,b,d a,c,d b,c,d a,b,c,d |
|
|
Permutation |
from itertools import permutations P = permutations([1,2,3]) for i in list(P): print(i) |
(1, 2, 3) (1, 3, 2) (2, 1, 3) (2, 3, 1) (3, 1, 2) (3, 2, 1) |
|
|
Sélection Ici 2 parmi 3. |
from itertools import permutations P = permutations([1,2,3],2) for i in list(P):
print(i) |
(1, 2) (1, 3) (2, 1) (2, 3) (3, 1) (3, 2) |
|
|
Comparaison |
||
|
Permutation (L, k) Combinaison (L, k) Notez l'orthographe de combination en anglais. |
from itertools import permutations,combinations A = [1, 2, 5] L = [] P = permutations(A) L.extend(P) print(len(L),L) M = [] Q = combinations(A,3) M.extend(Q) print(len(M),M) L = [] P = permutations(A,2) L.extend(P) print(len(L),L) M = [] Q = combinations(A,2) M.extend(Q) print(len(M),M) |
|
|
Permutation Combinaison 3 Permutation 2 Combinaison 2 |
6 [(1, 2, 5), (1, 5, 2), (2, 1, 5),
(2, 5, 1), (5, 1, 2), (5, 2, 1)] 1 [(1, 2, 5)] 6 [(1, 2), (1, 5), (2, 1), (2, 5), (5,
1), (5, 2)] 3 [(1, 2), (1, 5), (2, 5)] |
|
|
Accès à une permutation ou une combinaison de
rang k Accès direct impossible ! Il faut calculer toute la liste. Pourquoi ? Combinaison et permutation retournent des itérateurs, et
non des listes indexables directement. |
rom itertools import permutations, combinations A = [1, 2, 3, 4] P = list(permutations(A)) print("Permutation rang 2
:", P[2]) C = list(combinations(A, 3)) print("Combinaison rang 2
:", C[2]) |
|
|
Permutation rang 2 : (1, 3, 2, 4) Combinaison rang 2 : (1, 3, 4) |
||
|
Même chose sur une seule ligne |
from itertools import permutations, combinations A = [1, 2, 3, 4] print(list(permutations(A))[2]) print(list(combinations(A,3))[2]) |
|
|
|
(1, 3, 2, 4) (1, 3, 4) |
|
|
Anagrammes du nombre 1123 et liste des nombres
premiers parmi eux |
from itertools import permutations from sympy import isprime def ANA(n):
chiffres = list(str(n))
anagrammes = set()
for k in range(1, len(chiffres)+1):
for p in permutations(chiffres, k): anagrammes.add(int(''.join(p)))
return sorted(anagrammes) def PREM(n):
return [x for x in ANA(n) if isprime(x)] def main():
n = 1123
tous = ANA(n)
premiers = PREM(n)
print(f"Anagrammes de {n} ({len(tous)} au total) :")
print(tous)
print(f"Nombres premiers parmi eux \ ({len(premiers)}) :")
print(premiers) if __name__ == "__main__":
main() |
|
|
Anagrammes de 1123 (34 au total) : [1, 2, 3, 11, 12, 13, 21, 23, 31, 32, 112,
113, 121, 123, 131, 132, 211, 213, 231, 311, 312, 321, 1123, 1132, 1213,
1231, 1312, 1321, 2113, 2131, 2311, 3112, 3121, 3211] Nombres premiers parmi eux (18) : [2, 3, 11, 13, 23, 31, 113, 131, 211,
311, 1123, 1213, 1231, 1321, 2113, 2131, 2311, 3121] |
||
|
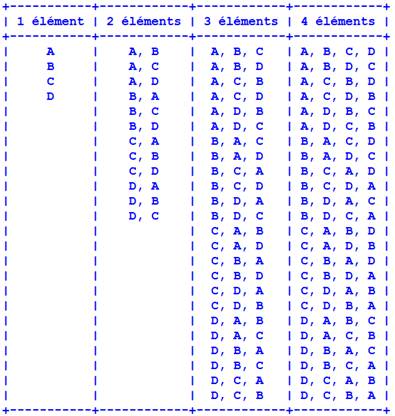
Toutes les permutations de quatre éléments & Affichage en table Nécessite l'import de prettytable avec: pip install
prettytable Remarque Table pas facile à créer et à manipuler! Je préfère importer les valeurs dans un traitement de texte et
convertir en tableau sur place. |
from itertools import permutations from prettytable import PrettyTable elements = ["A", "B", "C", "D"] # Préparer les colonnes table = PrettyTable() table.field_names = ["1 élément", "2 éléments", "3 éléments", "4 éléments"] # Trouver le nombre max de permutations max_len = max(len(list(permutations(elements, r))) for r in range(1, 5)) # Remplir les colonnes avec les
permutations rows = [] for i in range(max_len):
row = []
for r in range(1, 5):
perms = list(permutations(elements, r))
if i < len(perms): row.append(", ".join(perms[i]))
else:
row.append("") # case vide si pas assez de
permutations
rows.append(row) # Ajouter les lignes au tableau for row in rows:
table.add_row(row) print(table) |
|
|
|
||
Voir Affichage en Python
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()