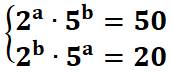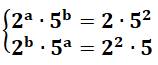Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 19/02/2024 M'écrire Brèves de Maths

INDEX Équations Algèbre Énigmes	Algèbre – Défis
	INDEX – Défis-Algèbre	50^99 et 99!	Divers défis 01
	Division fractions	Équation: x^4 + 4x -1 = 0	Équations en x, y, z
	Équation x^6 = (x – 1)^6	Équation: 2^a + 2^b + 2^c = 148	Équations en x^k, y^k, z^k
	Équation x^x^6 = 144	Factorielles	Équation: 2^a.5^b = 50 & 2^b.5^a = 20
			Équation: a√a+b√b et b√a+a√b

Équation 2^a٠5^b = 50 & 2^b٠5^a = 20 Comment résoudre ce système de deux équations ? Trois méthodes.
	Sommaire de cette page >>> Première méthode >>> Deuxième méthode >>> Troisième méthode	Débutants Base de l'algèbre Glossaire Équations

Première méthode		haut
Résoudre ce système d'équations en puissances de 2 et de 5.
La première idée consiste à factoriser ces deux nombres. Alors la solution est évidente: a = 1 et b = 2.

Deuxième méthode		haut
Prenons le logarithme des membres de ces équations. Se souvenir que: ln(x^y) = y ln (x) ln(x٠y) = ln(x) + ln(y) Là aussi, la méthode devient évidente en comparant les membres de droite de gauche.

Troisième méthode		haut
Même passage par les logarithmes que ci-dessus. Mais, appliqué au produit des deux égalités, puis à son quotient. L'un donne la somme des deux inconnues a et b et l'autre la différence. En additionnant ou en soustrayant ces valeurs, on isole soit a soit b. On utilise les logarithmes à base 10. Si bien que log(10) = 1 et log(1000) = 3. La somme des logarithmes de 2 et 5 est le log de 10. Les différences des logarithmes de 2 et 5 se simplifient naturellement.

Haut de page

Retour	Algèbre – Index Énigmes – Index
Suite	Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Algebre/Equa2a5b.htm