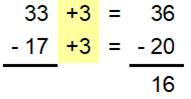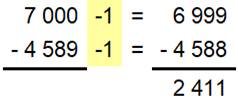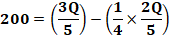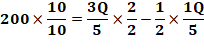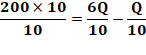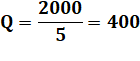|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Apprentissage du calcul Méthode de Singapour Formellement la méthode dite
de Singapour est originale. Pourtant, elle fait appel à des notions pratiques
qui faisaient partie de l'enseignement du calcul tel que pratiqué
d'autrefois:
Je ne suis ni enseignant, ni pédagogue. Ces pages
sont une compilation de ce que j'ai compris de la méthode à l'usage de qui
voudrait avoir une petite idée de cette pédagogie. Son efficacité réside sans
doute dans le soin et la rigueur apportés à son application. |
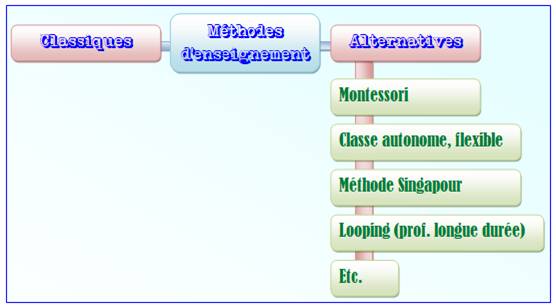
Principales
méthodes d'enseignement
|
Parmi
les méthodes flexible, la méthode indienne dite Teaching
At the Right Level (TARL). Contrairement
aux approches traditionnelles, la méthode TARL se focalise sur l’adaptation
des acquis en fonction du niveau des élèves, le « ré-enseignement » des
compétences fondamentales en fonction du niveau réel des élèves, afin de
combler les lacunes accumulées. On
n'est pas loin de la notion de groupes de niveau
en France. |
Situation géographique de SINGAPOUR
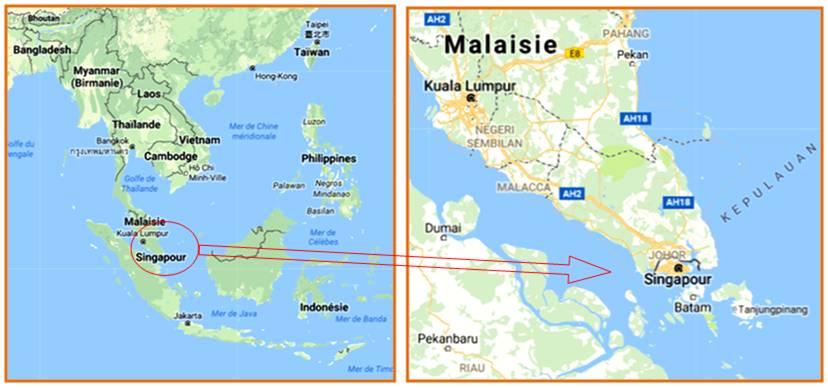
Je
ne résiste par à situer Singapour, ce tout petit pays très dynamique où j'ai
maintes fois mis les pieds.
Quizz:
sauriez-vous montrer la Malaisie, toute la Malaisie? Bravo: il y a bien deux
parties bien séparées
Voir Marina Bay
Sands / Géographie – Index
![]()
|
|
||
|
Étape concrète Comptage
des bonbons
|
Je compte 1,
2, 3, 4, 5, 6 bonbons
|
|
|
Étape abstraite Addition
des groupes de points |
2 +
2 + 2
= 6
|
|
|
Introduction d'un nouveau concept Le signe
multiplié |
3 x 2 =
6
|
|
Point
|
L'idée consiste à
introduire des observations sans donner la procédure de calcul qui sera expliquée
dans un deuxième temps, après une bonne assimilation du procédé de comptage.
Il s'agit essentiellement de visualiser les nombres, de les apprivoiser. On
pratique les calculs avant d'analyser leurs principes. Analogie: l'enfant
utilise automatiquement les verbes conjugués. Il apprend la grammaire et la
conjugaison que bien après. |
Voir Brève
55-1095
|
La
méthode des relations entre nombres (number bond ou
addition fact) |
|
|
|
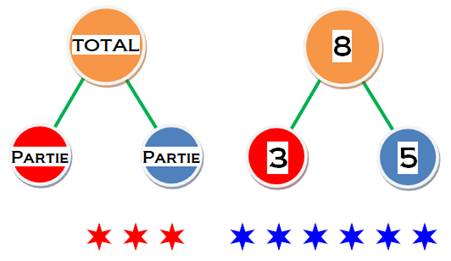
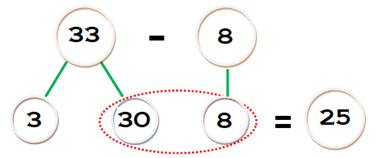
Étape 1) donner la relation entre trois nombres: le total étant composé de
deux parties. Si on
compte les étoiles (ou autres choses), on retrouve les trois nombres (sans,
pour le moment) parler d'addition. |
Principe & Exemple
|
|
|
Étape2) additions et soustractions avec ces trois nombres. Pour
l'élève la relation entre addition et soustraction devient implicite (sans la
nommer). |
3 + 5 =
8 8 – 3 = 5 5 + 3 =
8 8 – 5 = 3 Ces deux
opérations et leurs commutations sont lisibles
sur le schéma de liens. |
|
|
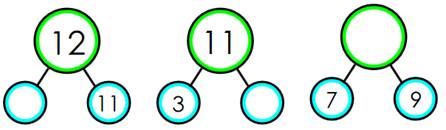
Partition et addition Automatismes
de l'addition des petits nombres |
Cette partie de la méthode (number bond) introduit ce formalisme à
trois cercles qui, finalement, fait pratiquer la table d'addition. Le but est
de créer des réponses spontanées pour les opérations les plus simples. |
|
|
Opérations à trous Exemples
de calculs proposés. |
|
|
|
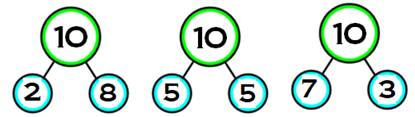
Connaissance
indispensable pour effectuer le calcul
mental (Voir
ci-dessous). Voir Tout sur le nombre
10 |
|
|
|
|
||
|
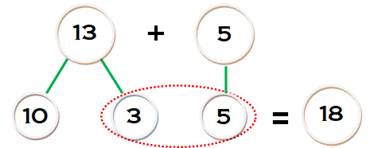
Addition sans retenue Mentalement,
13 est partitionné en 10 et 3; le 3 est ajouté au 5 pour faire 8. La somme
est égale à 10 + 8 = 18. Plus
simplement, on se contente d'ajouter les unités. |
|
|
|
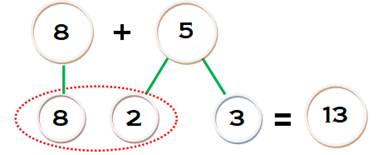
Addition avec retenue Mentalement,
5 est partitionné en 2 et 3 de sorte que le 2 complémenté à 8 donne 10. La
somme est 10 + 3 = 13. |
|
|
|
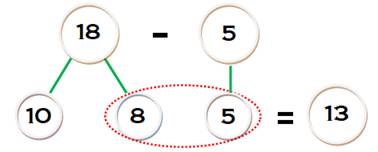
Soustraction sans retenue Mentalement,
18 est partitionné en 10 et 8; du 8 on ôte 5 pour faire 3. La différence est
égale à 10 + 3 = 13. Plus
simplement, on se contente de soustraite les unités. |
|
|
|
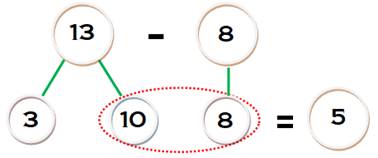
Soustraction avec retenue Mentalement,
18 est partitionné en 10 et 8; du 8 on ôte 5 pour faire 3. La différence est
égale à 10 + 3 = 13. Autre possibilité (à la française): Différence
entre 8 et 13 = déjà 2 pour atteindre 10
puis 3 pour aller jusqu'à 13, au total ça
fait 5. Différence
entre 8 et 33: on compte mentalement 3 pour aller à 10, puis 20 pour aller à
30 et 3 pour finir. Soit 2 + 20 + 3 = 25 |
|
|
|
Objectif:
remplacer une soustraction par une autre plus simple. Principe: ajouter
aux deux termes un nombre produisant un complément à un nombre rond ou
"casser" un nombre rond.
|
Divisions rapides
|
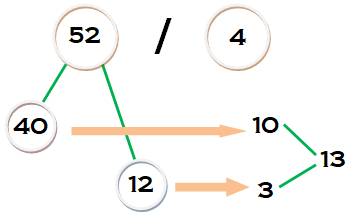
Objectif: partager
le nombre en deux parts dont l'une est en dizaines, multiple du diviseur Principe: diviser
chaque part par le diviseur et ajouter les résultats.
|
|
(Bar model ou strip diagram) |
|
|
|
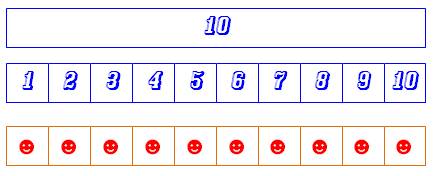
Visualisation des nombres de 1 à 10
par des barres Ces
barres procurent une vision concrète des nombres. Elles
montrent comment les nombres peuvent être composés de parties. |
|
|
|
Représentation Un nombre est représenté par une barre d'une
certaine longueur. Cette
barre est divisée en unités. Une
représentation concrète peut y être associée (relation cardinal et
ordinal). |
|
|
|
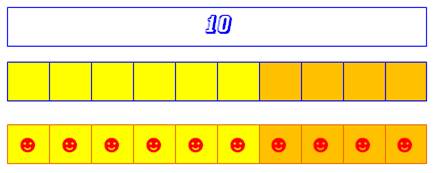
Total et parties Représentation
de l'opération 10 = 6 + 4 On
retrouve, sous une autre forme, la représentation précédente dite
"number bond" |
|
|
|
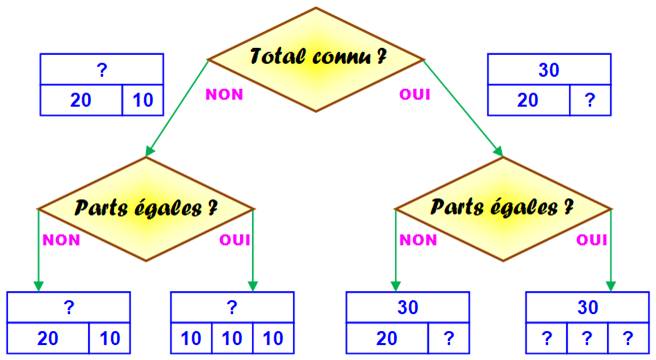
Les quatre opérations selon les
nombres connus
|
||
|
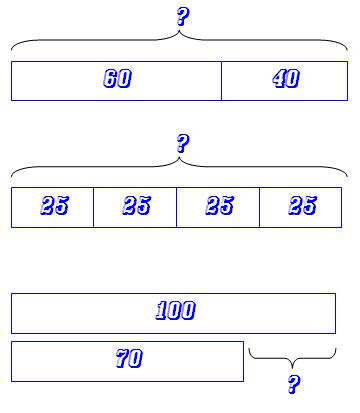
Exemples de calculs visualisés 1)
Calculer la somme 60 + 40 2)
Calculer le produit 4 x 25 3)
Calculer la différence 100 – 70 |
|
|
|
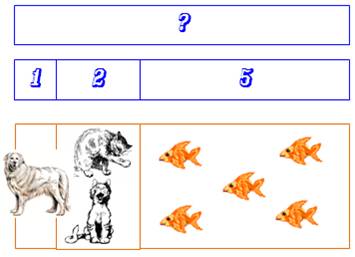
Exemple d'addition Nathan a
un chien, deux chats et cinq poissons rouges. Combien
a-t-il d'animaux? 1 + 2 + 5
= 8 |
|
|
|
|
||
|
Problème Nathan et
Alexis ont un total de 180 euros dans leur tirelire. Nathan,
l'aîné, a 22 euros de plus qu'Alexis Combien
chacun a-t-il dans leur tirelire? |
Nathan et Alexis
possèdent 180 € |
|
|
Représentation Application
de la méthode des barres. Visualisation
arithmétique de la situation. |
|
|
|
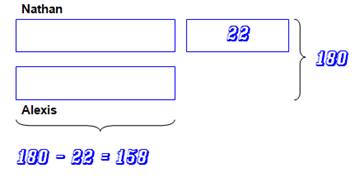
Calculs Les deux
barres identiques représentent deux fois la somme d'Alexis et elle vaut 158 La somme
d'Alexis vaut 158 / 2 = 79 euros. La somme de
Nathan vaut 79 + 22 = 101 euros. |
|
|
Anglais pour tirelire: piggy box
|
|
||
|
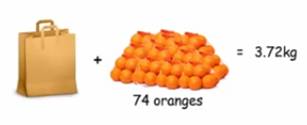
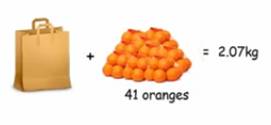
Problème Nathan
achète des oranges et les met dans son propre sac. Il constate que:
Il se
demande quel est le poids de son sac, tout seul, en grammes. Note: les oranges sont identiques. Poids est l'usage courant du terme masse qui
devrait figurer ici. |
|
|
|
Représentation Application
de la méthode des barres. Visualisation
arithmétique de la situation. |
|
|
|
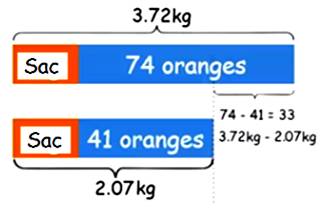
Calculs On
calcule d'abord le poids d'une orange. Puis le
poids de 41 oranges + sac qui permet de trouver le poids du sac par simple
soustraction. |
33 oranges pèsent 3,72 – 2,07 = 1, 65 kg 1 orange
pèse 1,65 / 33 = 0,05 kg Sac + 41 oranges
= 2,07 kg Sac + 41 x 0,05 = 2,07 Sac + 2,05 = 2,07 Sac + 2,05 – 2,05 = 2,07 – 2,05 Sac = 0,02 kg = 20 g |
|
|
|
||
|
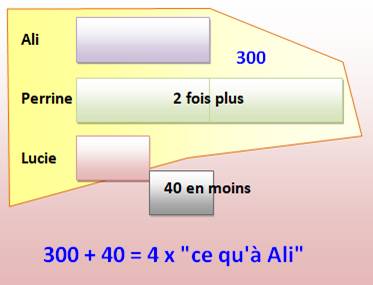
Problème Perrine a
deux fois plus d'autocollants qu'Ali. Ali a 40
autocollants de plus que Lucie. À eux
trois, ils ont 300 autocollants en tout. Combien
d'autocollants Perrine possède-t-elle ? Solution (Voir illustration) 4 fois ce
qu'à Ali = 340 Ce qu'à
Ali = 340 / 4 = 85 Ce qu'à
Perrine = 2 x 85 = 170 Ce qu'à
Lucie = 85 – 40 = 45 |
Illustration
|
|
Problème typique – Le Point – Maths, la
méthode Singapour – Octobre 2017
|
|
||
|
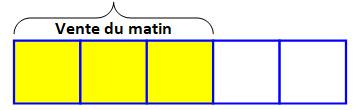
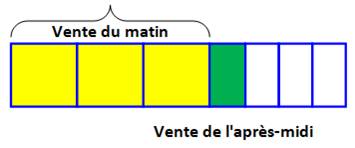
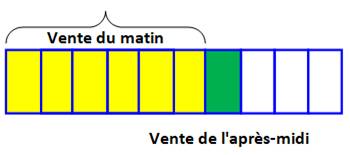
Problème Nathan
vend ses oranges. Il en
vend les 3/5 le matin et un quart du reste dans l'après-midi. Il en a
vendu 200 de plus le matin que l'après-midi. Combien
avait-il d'oranges pour commencer la journée? |
|
|
|
Égalisation On
partage la barre en parts égales. (réduction
au même
dénominateur sans la nommer) On note
qu'il y a 6 cases jaunes pour une verte; soit, 5 cases de plus en jaune qu'en
vert. |
|
|
|
Raisonnement Nathan
vend 200 oranges en plus le matin; elles correspondent aux 5 cases jaunes en
plus |
200 oranges pour 5 cases 200 / 5 = 40 oranges par case Total des oranges le matin: 10 cases x 40 = 400 oranges |
|
|
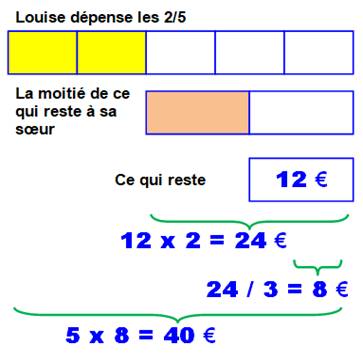
Autre exemple Louise
dépense les 2/5 de son argent et donne la moitié de ce qui reste à sa sœur.
Finalement, il lui reste 12 euros. Combien
avait-elle d'argent? Solution Visualisation
avec des barres partagées en 5 pour la première et en 2 pour la seconde. Connaissant
la partie qui reste (12), on remonte: la seconde barre vaut 24 et chaque
partie de la première barre vaut 8. Soit la valeur de la première barre: 40
euros. |
|
Voir Fractions débutants
|
|
|||
|
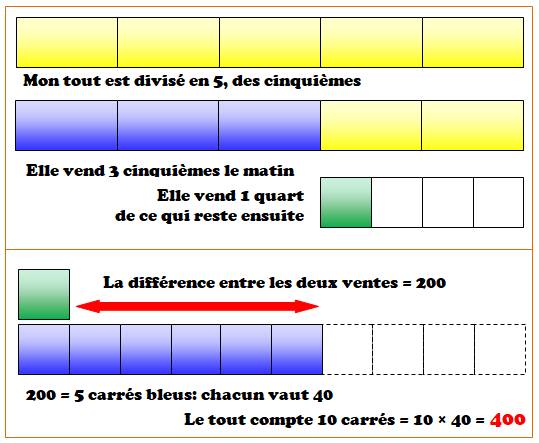
Problème Emma vend des tartelettes.
Elle en a vendu 3/5 le matin et 1/4 des tartelettes restantes l’après-midi.
Si elle a vendu 200 tartelettes de plus le matin que l’après-midi, combien de
tartes avait-elle au début? Idée Faire la différence entre la
quantité vendue le matin (trois cinquième
de Q, la quantité totale) avec la quantité vendue l'après-midi. |
Résolution classique (pas à pas)
|
||
|
Résolution visuelle (Singapour) On commence à visualiser les 3 cinquièmes (bleu) du tout (jaune), puis
on montre le quart de ce qui reste (vert). En, bas, on met en évidence la différence entre la vente du matin
(bleue) et celle de l'après-midi (vert). Elle vaut 200 tartelettes et correspond à 5 carrés bleus. Or, le tout est formé de deux fois cinq carrés et le double de 200 est
400. |
|
||
Source de cet exemple: Monica
Neagoy, auteur de La nouvelle édition de la méthode de Singapour
– Présenté par BFM TV. – 09/04/2019
Voir Problèmes à
la mode sur Internet
|
En gros, la méthode Singapour dit: soyons
concrets avant de passer à l'abstrait. Rien ne vaut une bonne représentation
imagée pour compter et calculer. Le modèle à barre permet l'assimilation
instinctive des notions de fractions
et de ratios,
tout comme des rudiments de l'algèbre. Priorité
est donnée à la maitrise d'un minimum de concepts et non à la mémorisation
(apprentissage par cœur). On comprend; on n'applique pas des recettes. Autre élément fondamental: le travail en petits
groupes est favorisé. Les élèves s'expliquent entre eux. Les erreurs et le
tâtonnement font partie de la pédagogie. Les méthodes de Singapour, de Jérôme Bruner ou de
Maria Montessori s'inspirent toutes de la même veine. |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()