|
|||||||||||||||||||||||||||||||||||||
![]()
|
Nombres composés jamais-premiers ou composés stables |
||
|
Multi-Premier
M (MPM) Il s'agit de
considérer tous les nombres formés en modifiant l'un des chiffres tout en
conservant les autres. Avec un nombre à
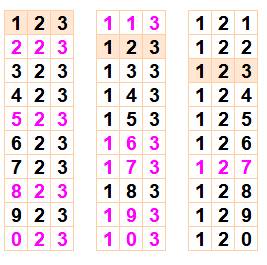
trois chiffres distincts comme 123, il y a 28 nombres possibles (le nombre
123 se retrouve trois fois dans le tableau). En rose, les dix
nombres premiers. Le nombre 123 est un multi-premier
par modification des chiffres. |
|
|
|
Composés
stables ou Il existe des
nombres pour lesquels aucune configuration n'est première. C'est le cas de
cet exemple avec le nombre 326. Toutes les configurations
avec 6 pour unité sont divisibles par 2. Dans la colonne
de droite, outre les nombres divisibles par 2 et 5, il reste 4 nombres qui
s'avèrent, eux-aussi, composés. |
|
|
|
ou composés stables |
||
|
Jamais-Premier
M (JPM) Le plus petit est 200. Ils sont 95
jusqu'à 1 500. Il y en a une
infinité (prouvé). |
200,
204, 206, 208, 320, 322, 324, 325, 326, 328, 510, 512, 514, 515, 516, 518,
530, 532, 534, 535, 536, 538, 620, 622, 624, 625, 626, 628, 840, 842, 844,
845, 846, 848, 890, 892, 894, 895, 896, 898, 1070, 1072, 1074, 1075, 1076,
1078, 1130, 1132, 1134, 1135, 1136, 1138, 1140, 1142, 1144, 1145, 1146, 1148,
1260, 1262, 1264, 1265, 1266, 1268, 1330, 1332, 1334, 1335, 1336, 1338, 1340,
1342, 1344, 1345, 1346, 1348, 1350, 1352, 1354, 1355, 1356, 1358, 1410, 1412,
1414, 1415, 1416, 1418, 1460, 1462, 1464, 1465, 1466, 1468, 1500, … |
|
|
Autres
que divisibles |
212159,
294001, 505447, 584141, 595631, 604171, 872897, 971767, 1062599, 1203623,
1282529, 1293671, 1524181, 1566691, 1702357, 1830661, 2017963, 2474431,
2690201, 3085553, 3326489, 3716213, 3964169, 4103917, 4134953, 4173921,
4310617, 4376703, … |
|
Voir Brève 721
![]()
|
Retour |
|
|
Suite |
· Suite de nombres composés consécutifs · Suite
de nombres composés: 381, 3811 … · Nombres composés –
Caractérisation · Premiers
– Index · Types ne nombres composés
selon leurs facteurs · Plus petit nombre composé ou premier? · Nombres de Cullen et de Woodall
– majoritairement composés |
|
Voir |
·
Nombre - Glossaire ·
Types de nombres selon leurs
diviseurs ·
Théorème
fondamental et sa démonstration |
|
DicoNombre |
|
|
Sites |
·
OEIS A118118 – Composite numbers that
always remain composite when a single decimal digit of the number is changed ·
OEIS A186694 - Numbers ending in 1, 3, 7
or 9 such that changing any one decimal digit produces a composite number. |
|
Cette page |
![]()