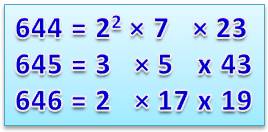Quantité de facteurs distincts pour une suite de nombres

Approche		haut
Exemple avec nombre de 20 à 30 Le nombre 20 possède deux facteurs distincts (trois au total). Les nombres 21 et 22 en ont deux aussi. Nous tenons là une suite de trois nombres consécutifs ayant la même quantité (2) de facteurs distincts. C'est la plus petite possibilité. La suite suivante avec quatre nombres consécutifs et deux facteurs distincts est: 33, 34, 35, 36. Fonction arithmétique La quantité de facteurs distincts a pour symbole:	Nombre, quantité de facteurs distincts et factorisation
Nombres de 1 à 100 On donne successivement la longueur de la suite la quantité de facteurs communs la liste des nombres de la suite. Naturellement, la première suite comporte quatre nombres (2, 3, 4, 5) avec des nombres à un seul facteur. Le nombre suivant (6) brise la suite avec deux facteurs. En dernière ligne, le nombre 91 débute une suite de six nombres ayant deux facteurs distincts.	4, 1, [2, 3, 4, 5] 3, 1, [7, 8, 9] 2, 2, [14, 15] 2, 1, [16, 17] 3, 2, [20, 21, 22] 2, 1, [31, 32] 4, 2, [33, 34, 35, 36] 3, 2, [38, 39, 40] 3, 2, [44, 45, 46] 3, 2, [50, 51, 52] 5, 2, [54, 55, 56, 57, 58] 2, 2, [62, 63] 2, 2, [68, 69] 4, 2, [74, 75, 76, 77] 4, 2, [85, 86, 87, 88] 6, 2, [91, 92, 93, 94, 95, 96]

Records pour deux facteurs distincts

haut

Suite de nombres à deux facteurs distincts

Chaque ligne constitue un record: la plus petite suite ayant k facteurs distincts.

Records (seuls cas jusqu'à 1 million)

2, [14, 15]

3, [20, 21, 22]

4, [33, 34, 35, 36]

5, [54, 55, 56, 57, 58]

6, [91, 92, 93, 94, 95, 96]

8, [141, 142, 143, 144, 145, 146, 147, 148]

Records pour trois facteurs distincts

haut

Suite de nombres à trois facteurs distincts

Chaque ligne constitue un record: la plus petite suite ayant k facteurs distincts pour k croissant.

Têtes de liste

30, 230, 644, 1308, 2664, 6850, 10280, 39693, 44360, 48919, 218972, 526095, 526095, 526095, 17233173, 127890362, 29138958036, 146216247221, …

Le suivant, s'il existe, est supérieur à 1,1 10¹².

Têtes de liste pour suite de 3 nombres à trois facteurs distincts:

644, 740, 804, 986, 1034, 164, 1104, 1220, 1274, 1308*, 1462, 1494,1580, 1746, 1884*, 1924, 1988, 2013*, …
* avec quatre nombres

Records (seuls cas jusqu'à 1 million)

2, [230, 231]

3, [644, 645, 646]

4, [1308, 1309, 1310, 1311]

5, [2664, 2665, 2666, 2667, 2668]

6, [6850, 6851, 6852, 6853, 6854, 6855]

7, [10280, 10281, 10282, 10283, 10284, 10285, 10286]

8, [39693, 39694, 39695, 39696, 39697, 39698, 39699, 39700]

9, [44360, 44361, 44362, 44363, 44364, 44365, 44366, 44367, 44368]

10, [48919, 48920, 48921, 48922, 48923, 48924, 48925, 48926, 48927, 48928]

11, [218972, 218973, 218974, 218975, 218976, 218977, 218978, 218979, 218980, 218981, 218982]

14, [526095, 526096, 526097, 526098, 526099, 526100, 526101, 526102, 526103, 526104, 526105, 526106, 526107, 526108]

Voir Brève 52-1020

Records pour quatre facteurs distincts

haut

Suite de nombres à quatre facteurs distincts

Chaque ligne constitue un record: la plus petite suite ayant k facteurs distincts.

Records (seuls cas jusqu'à 1 million)

2, [7314, 7315]
7314 = 2 × 3 × 23 × 53
7315 = 5 × 7 × 11 × 19

3, [37960, 37961, 37962]

4, [134043, 134044, 134045, 134046]

5, [357642, 357643, 357644, 357645, 357646]

Records pour cinq facteurs et plus distincts

haut

Suite de nombres à cinq facteurs et davantage

En tête des crochets, la quantité de facteurs distincts.

En fait, uniquement 5.

Records (seuls cas jusqu'à 350 millions)

2, [5, 254540, 254541]

3, [5, 1042404, 1042405, 1042406]

4, [5, 21871365, 21871366, 21871367, 21871368]

5, [5, 129963314, 129963315, 129963316, 129963317, 129963318]

Somme des quantités de facteurs distincts

haut

Exemple pour S = 10

Oméga est la quantité de facteurs distincts. Leur somme pour quatre nombres consécutifs est égale à 10. Le plus petit cas.

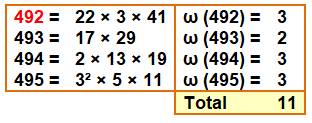
Exemple pour S = 11

Oméga est la quantité de facteurs distincts. Leur somme pour quatre nombres consécutifs est égale à 11. Le plus petit cas.

Exemple pour S = 12

Oméga est la quantité de facteurs distincts. Leur somme pour quatre nombres consécutifs est égale à 12. Le plus petit cas.

Plus petit pour S successifs

S = 3 pour le premier nombre de la liste (1).

On retrouve 987 pour S = 12.

1, 2, 3, 9, 12, 33, 75, 153, 492, 987, 4179, 13803, 18444, 134043, 282489, 1013724, 4289592, 12582633, 57495513, 260628717, 801621093, 3307216989, 5313193818, 62909521245, 308935340153, 611063815284, …

OEIS A175206

Haut de page (ou double-clic)

Suite	Nombres consécutifs avec même quantité de facteurs (tous) Liste de facteurs premiers pour n > 100 Types de nombres selon leurs diviseurs Nombres égaux à la somme des premiers situés entre ses facteurs extrêmes Voir en haut de page Liste des nombres et leurs facteurs et diviseurs
Voir	Calcul mental – Index Conjecture ABC Divisibilité Machine des frères Carissan Nombres composés PGCD Premiers Théorie des nombres – Index
Sites	OEIS A064708 – Initial term of run of (at least) n consecutive numbers with just 2 distinct prime factors OEIS A080569 – a(n) is the first number in the first run of at least n successive numbers, all having exactly 3 distinct prime factors
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/QFacteur.htm