NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/05/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Introduction à la Théorie des nombres
Débutants Division	DIVISEURS				Glossaire Division
INDEX Accueil Sommaire	Introduction	Valeurs	Quantité	Somme
		Produit	Comparaisons	Som-Prod
		Sommaire de cette page >>> Exemple avec 100 >>> Nombres de 1 à 100 >>> Programmation

SOMME & PRODUIT des DIVISEURS

Comparaison des sommes partielles des diviseurs et du produit correspondant. Maximum ?

Un nombre dont une somme partielle des diviseurs est égale au nombre est un nombre pseudo-parfait (ou semi-parfait).

Exemple avec 100

Carte d'identité du nombre 100

100 = 10²	Facteurs	100 = 1 x 2² x 5²
	Diviseurs	1, 2, 4, 5, 10, 20, 25, 50, 100
	Quantité	9
	Somme	217
	S - N	117 > 100 (abondant)
	Produit des facteurs uniques	2 x 5 = 10
	Produit des diviseurs et son mode de calcul	1 000 000 000

Partition la plus généreuse (conduisant au plus grand produit)

Partition: 100 = 32 x 3 + 2 x 2

Produit: 3³² x 2² = 7 412 080 755 407 364 (avec le maximum de 3)

Comparaison: 2⁵⁰ = 1 125 899 906 842 624 (avec les 2 seulement).

Voir Partitions généreuses

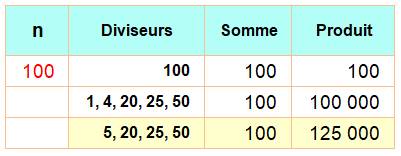
Diviseurs dont la somme est 100

Trois configurations dont une triviale.

Le troisième conduit au produit maximum.

Quantité de sommes partielles

Avec neuf diviseurs, la quantité de sommes partielles des diviseurs est égale à 2⁹ = 512.

Avec tous les diviseurs (ou même sans le 1), le produit est égal à 10⁹, le maximum.

Avec deux diviseurs le maximum est: 50 x 10 = 500.

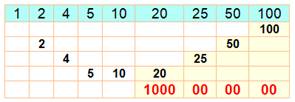
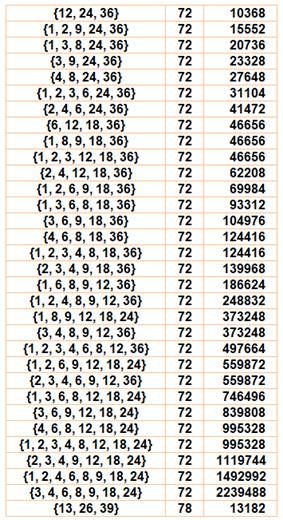
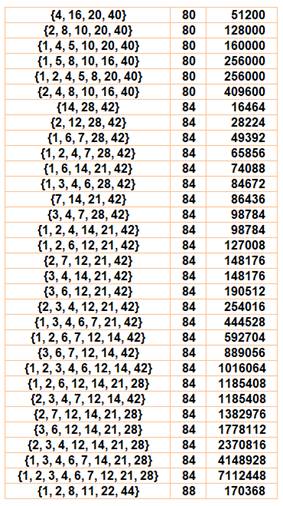
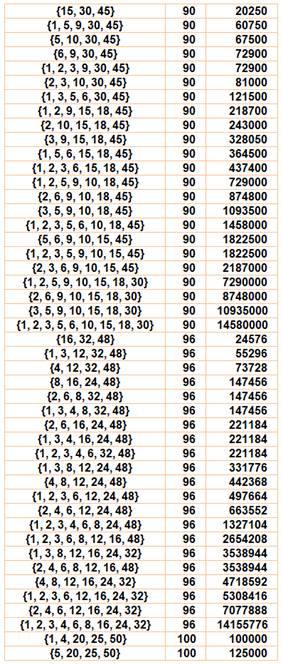
Exemples de sommes partielles et produits correspondants:

{Diviseurs}, somme, produit

{2 , 4} , 6 , 8

{2 , 5} , 7 , 10

{2 , 10} , 12 , 20

{2 , 20} , 22 , 40

{2 , 25} , 27 , 50

{2 , 50} , 52 , 100

{2 , 100} , 102 , 200

{4 , 5} , 9 , 20

{4 , 10} , 14 , 40

{4 , 20} , 24 , 80

{4 , 25} , 29 , 100

{4 , 50} , 54 , 200

{4 , 100} , 104 , 400

{5 , 10} , 15 , 50

{5 , 20} , 25 , 100

{5 , 25} , 30 , 125

{5 , 50} , 55 , 250

{5 , 100} , 105 , 500

Voir Nombre 100

Somme diviseurs = n – Avec n de 1 à 100
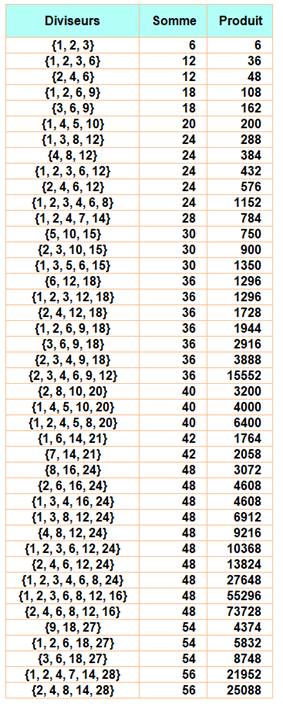
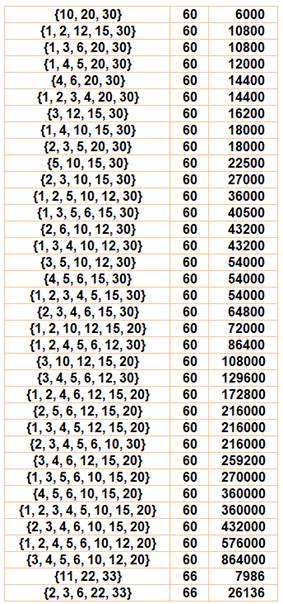
Peu d'élus et tous pairs. Souvent avec de très nombreuses configurations comme 60 avec 36 configurations. Nombres dont la somme des diviseurs est égale au nombre [6, 12, 18, 20, 24, 28, 30, 36, 40, 42, 48, 54, 56, 60, 66, 72, 78, 80, 84, 88, 90, 96 100] Liste

Programmation – Recherches des nombres pseudo parfaits, des configurations et des produits
	Commentaires Appel des logiciels de théorie des nombres et de combinatoire. Analyse des nombres de 1 à 20. Pour chacun, liste des diviseurs en Div et de toutes les combinaisons partielles en S. Tant que (while) la liste S n'est pas épuisée, on analyse chaque configuration de la liste en suivant (nextvalue). Produit des diviseurs partiels en M et leur somme en A. Si la somme A vaut n et si le cas n'est pas trivial (somme de deux termes au moins), alors impression. Fin de condition (fi). Et fin des boucles (od). En bleu, résultat du traitement. On note le cas du nombre 6 qui est pseudo-parfait par la somme et parfait par le produit. Le nombre parfait suivant est 28, mais sa configuration pseudo parfaite est 28, {1, 2, 4, 7, 14}, 28, 784} qui ne donne pas le produit parfait.

Voir Programmation – Index

Retour Suite	Diviseurs – Somme Diviseurs – Produit Diviseurs – Quantités Diviseurs – Comparaison Facteur le plus grand
Voir	Calculs avec les diviseurs Diviseurs Types de nombres selon diviseurs Somme en puissances Théorie des nombres – Index Jeux et puzzles – Index
Sites	OEIS A005835 – Pseudoperfect (or semiperfect) numbers n: some subset of the proper divisors of n sums to n.
Cette page	http://villemin.gerard.free.fr/Referenc/Prof/APROF/Somprod.htm