NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/01/2016 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Mathématiques
Débutants Général	OUTILS			Glossaire Général
INDEX Théorie des nombres	Index	Diagonale de Cantor	Valeurs intermédiaires
		Sommaire de cette page >>> Approche >>> En binaire infini >>> Infini plus un? >>> Rationnels et réels

Outil: DIAGONALE de CANTOR

Comment faire la liste de tous les nombres et, pourtant, en trouver encore d'autres… Conclusion: il existe plus d'un type d'infini ! Cantor est à l'origine de cette démonstration.

Voir Page miroir en Diagonale de Cantor

Approche
Choisissez quatre nombres de quatre chiffres et formez un nombre en considérant les chiffres de la diagonale pour choisir un chiffre différent (plus un par exemple). Nous venons de créer un nouveau nombre obligatoirement différent des précédents. Pourquoi? Le premier chiffre et différent de celui du premier nombre; Le deuxième chiffre est différent de celui du deuxième nombre; Etc. Au final, chaque chiffre du nouveau nombre est différent de celui d'un des nombres du tableau de départ.	4 5 6 7 2 3 8 9 9 8 7 6 5 5 5 5 5 4 8 6 Le nombre 5486 est un nouveau nombre, différent de ceux déjà dans le tableau. C'est le principe de la diagonale de Cantor (1845-1918).

En binaire … infini
On peut même utiliser les nombres exprimés en binaire: Simple commodité! Alors, on prend les chiffres sur la diagonale, en les inversant. Nous n'avons fait aucune restriction sur la quantité de chiffres (colonnes) et de nombres (lignes). Ça marche pour un tableau aussi grand que l'on veut; Même … infini! Quelle que soit la quantité de nombres que je pourrais mettre dans le tableau, il en existera toujours un autre différent de tous ceux-ci.	1 1 1 1 1 0 0 1 0 0 0 1 0 1 1 0 0 1 1 1 Aussi grand que l'on veut 1 1 1 1 … 1 0 0 1 … 0 0 0 1 … 0 1 1 0 … … 0 1 1 1 … Même infini!

OUP! Infini + 1 ?
Nous nous trouvons devant une espèce de paradoxe: Nous nous efforçons de mettre tous les nombres possibles et imaginables dans un tableau Et, pourtant, quoique l'on fasse, il en existera toujours un en plus. Cantor en déduit qu'il existe un infini plus grand, soit, plusieurs sortes d'infinis. De cette découverte, Cantor en fut lui-même étonné, voire effrayé. Tirons-en les conséquences pour les nombres réels…

RATIONNELS & RÉELS
Nous allons prendre les nombres décimaux compris entre 0 et 1: ceux qui commencent par 0, … Avec la règle de la diagonale de Cantor, il est toujours possible de former un nouveau nombre, quel que soit l'inventaire que nous puissions produire
Quelle est la propriété du nouveau nombre créé b? b est bien un réel compris entre 0 et 1 et, par construction il n'appartient pas au tableau de correspondance. C'est un nombre en plus! Nombres L'application de la diagonale de Cantor montre que le tableau ne contiendra jamais tous les nombres réels. On montre que: Les réels sont plus nombreux que les rationnels; il y en même beaucoup, beaucoup plus! Voir Diagonale des rationnels Ces deux ensembles ne sont pas équipotents (en bijection); Les réels font partie de l'ensemble 1 supérieur en cardinalité à 0 Voir hypothèse du continu Au delà? Oui! Il y a des infinis plus grands que les autres. Par exemple L'ensemble des courbes géométriques est plus grand que celui des points géométriques: On atteint un troisième ordre d'infini.	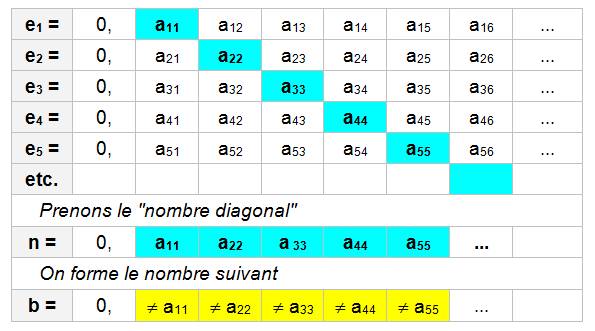Création de b Pour fixer les idées, on peut prendre bi = 2 si aii = 1 et bi = 1 si aii   1 Comparaison de b à e Si je compare b à e, il y aura au moins une ligne de e, quelque part, dans laquelle une des décimales sera différente. Exemple Pour e 3, et par construction, le troisième chiffre de b est différent du troisième chiffre de e3 b3 a33 Généralisation Ceci est vrai pour tous les chiffres de b. B est un nouveau nombre. Un nombre en plus.

Suite	Infini Inventaire des outils mathématiques – Index
Voir	Arbre de Stern-Brocot Compter les nombres Théorie des nombres – Index DicoMot DicoNombre
Cette page	http://villemin.gerard.free.fr/Referenc/Outils/Outils/DiagCant.htm