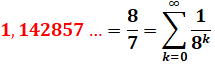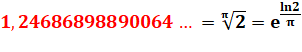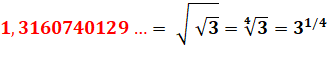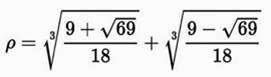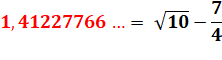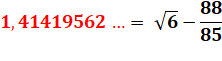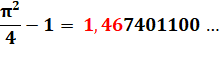NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 12/01/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres	DicoNombre NOMBRES			Glossaire Nombres
0,9 0,5 0,1 0,01 0,001 0	1			2 / 3 4 / 5 6 / 7 / 8 / 9 10 / 15 20 / 50 100 / 500 1000
Nombre 1	Culture 1	Maths 1	De 1 à 1,5	Expressions en 1
Débutant 1	Culture 1 suite	Unité	De 1,5 à 1,9	Proverbes en 1
Quiz 1	Quantité 1	Racines de 1	Fractions = 1
Sciences	Repunit	Nombres en 1	Fractions Unitaires

Il n'y a que deux racines carrées de nombres entiers qui commencent par 1.

= 1,4142 135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 7846210703 8850387534 3276415727 … >>>

= 1,7320 508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 1690880003 7081146186 7572485757… >>>

Voir Table des racines / Racine cinquièmes de 2 = 1, 148…

1,0

1,00…	Voir recherche de nombres presque entiers proches de1.
1,00…01^n	Donne les coefficients de la ligne n du triangle de Pascal.

Somme des inverses des puissances paires >>>

Physique

1,001 159 … Moment magnétique de l'électron.

>>>

1,003… = 253/252 = 1/2 + 1/4 + 1/7 + 1/9 = 1/3 + 1/4 + 1/6 + 1/7 + 1/9 = 1,00396825 396825 …	Meilleure approximation de 1 avec une somme des inverses des chiffres.
	Comma pythagoricien ou comma diatonique. Intervalle existant entre 7 octaves et 12 quintes pures. Il vaut environ 23,46 cents, soit presque un huitième de ton. Cet intervalle apparaît dans la construction de l'accord pythagoricien.
1,0185 185 … = 55 / 54	Fraction magique prétexte à une énigme.
1,036 … = 1,036 927 755 143 369...	Zêta 5, limite de la fonction de Riemann d'ordre 5. En 2018, cette constante est connue avec 20 milliards de décimales – Alexander Yee
	Somme des quatre premières fractions égyptiennes paires.
	Nombre irrationnel.

1 h 05 min 27,27 s

Première superposition des aiguilles de l'horloge.

1,0594… = 1,0594630943 5929526456 1825294946 3417007792 043174942…	La gamme tempérée divise l'octave en 12 intervalles chacun de cette dimension.
1,0606 ... = 1,0606601717 7982128660 1266543157 2735589272 539065327…	Longueur de l'arête du cube du " Prince Rupert ".
1,062 g / cm^3	Densité moyenne du corps humain.
	Exponentielle d'exponentielle …
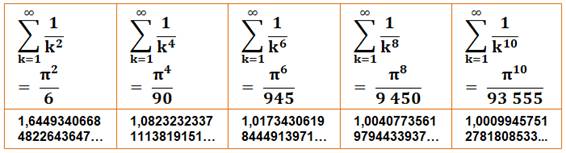
1,0823 ... = = = 1,0823232337 1113819151 6003696541 1679027747 509519187…	Zêta 5, limite de la fonction de Riemann d'ordre 5. Nombre transcendant. Ici, Pi est à la puissance 4, une puissance paire. On sait depuis Euler que toutes les suites en 2k s'expriment en p^2k, valeurs transcendantes.
	Somme des trois premières fractions égyptiennes.
1,08366 …	Constante de Legendre, conjecturée en1796.
	Somme des inverses des puissances de 12.
1,093 17… = lim. 1/S(n)!	Limite de cette série impliquant la fonction de Smarandache.
= 1,098684113… – i × 0,4550898605…	Combinaison de racine avec le nombre 2. Sert à calculer la racine de 1 – i (avec i² = -1).

1,1

Biologie	1,10 g / l Limite de glycémie sans risque de diabète.	>>>
Physique	1,1 ° Angle magique de supraconductivité du graphène. Deux couches superposées de graphène décalées de cet angle produit un effet de moire et surtout devient supraconducteur ou isolant selon la tension électrique appliquée à -270 °C.	>>>

	Soit deux nombres formés de 1. Trouver les deux exemplaires qui produisent le même résultat par l'addition et par la multiplication ? Voir Jeux avec les chiffres
	Somme des inverses des puissances de 11.
1,1^1/2 = 1,048808848	Curiosité: racine carrée de 1,1 avec des 4 et des 8.
1,111…= 10 / 9 = 1/10 + 1/100 + 1/1000 + ....	Nombre périodique en repunit. Voir illustration avec l'énigme de la Tablette de chocolat gratuite / Voir Puissances de 1,111. Cette forme donne les fractions dont le dénominateur est la suite des nombres impairs (ici le 9).
1,1,2 … 1 1 1 2 1 1 2 1 1 2 3	Série de Lionel Levine. Quelle est la suite ?
	Somme des inverses des puissances de 9. Aire maximale du carré le plus grand inscriptible dans un cube. Ses coordonnées: (1/4, 0, 0), (0, 1, 1/4), (3/4, 1, 1), (1, 0, 3/4),

	Somme des inverses des puissances de 8. Voir Nombre 142857
1,145 45… = 63 / 55	Nombre périodique
1, 148 … =	Taux de croissance conduisant à un doublement tous les cinq ans.
1,154 … = 1, 154 700 539 …	Tout ensemble (figure géométrique) de diamètre 1 peut être recouvert par un cercle de diamètre de cette taille - Théorème de Jung.
1,158…	Solution du problème de la chèvre dans un pré circulaire dont la loge est fixée à l'enclos. Avec cette valeur l'aire de la zone de broutage est moitié de celle du pré complet.
1,1666… = 1/2 + 2/3 = 7/6 = B14	Somme des fractions (1-1/2) et (1-1/3). Nombre de Bernoulli.

Économie

1,16675 euro = 1 dollar Parité de l'euro à son introduction en janvier 1999

>>>

1,176 …= Racine de F(x) = 1,176 280 81 …	Avec F(x) = x^10 + x^9 – x^7 – x^6 – x^5 – x^4 – x^3 + x + 1 La plus grande racine réelle. Nombre de Salem le plus petit connu.
1,189 … = = 2^1/4 = 1,189207115002721 …	Racine de racine de 2. Racine de F(x) avec F(x) => e^x (x – 1) = e^-x (x + 1). Nombre utilisé pour résoudre l'équation z – a = a sin z Stieltjes

1,2

	Somme des inverses des puissances de 6. Exemple de formulation avec le logiciel Maple
1,20205 … = (lire zêta 3) = 1,202 056 903 159 594 ... = 1 + 2^-3 + 3^-3 + 4^-3 + ... = 8/7 [1 + 3^-3 + 5^-3 + 7^-3 + ...] = 4/3 [1 - 2^-3 + 3^-3 - 4^-3 + 5^-3 - ...] = 5/2 [1/2 - (2!^2)/(4!2^3) + (3!^2)/(6!3^3) - (4!^2)/(8!4^3) + ...]	Constante d'Apéry: limite de la fonction de Riemann d'ordre 3. Irrationnel (démonstration par Apéry en 1978). Transcendant ? Suite en 1 / r^n: la somme de telles suites pour n pair est facile à calculer. Elle est de la forme multiple de ^n. Pour n impair, c'est beaucoup plus difficile! Connue en 1998 avec 32000279 décimales - Sebastian Wedeniwski – 35 heures de travail. Connue en août 2017 avec 500 milliards de décimales (Ron Watkins) Trois nombres choisis au hasard. La probabilité d'avoir des diviseurs communs est égale à 1 / ζ(3). Voir Nombre 0,831 / Constante Pi
1,2217293018702...	Limite de ln(3), ln(ln(3^3)), ln(ln(ln(3^33))), …
1,225 …	Fonction gamma.
1,226 …	Constante de factorielle Fibonacci.
1,23370055 …	Somme des inverses des impairs au carré.
1,234321 = 1,111²	Deux nombres voisins. Phi est le nombre d'or.
1,236067977 … =	Nombre qui commence par 123.

Biologie

1,24 En 2002: Nombre moyen de caries dentaires chez l'enfant de 12 ans.

>>>

Racine pi-ème de 2. Racine pi-ème de 4.

1,25 = 5 / 4			Somme des inverses des puissances de 5. Voir Chiffre 2
1,2539… =	Angle de l'heptagone régulier.
1,259 ... = = 1,259 921 049 894 873 164 76...	Constante de Délos ou Delian constant. Trouver le volume doublé du cube revient à déterminer la racine cubique de deux. Voir Duplication du cube  Racine réelle de x^3 – 2 = 0; il existe aussi deux autres racines complexes:
1,261 … = log4 / log 3 = 1,261 859 507 ...	Dimension du flocon ou courbe de Koch. Son périmètre est infini et son aire égale à 8/5 pour une aire initiale unité. Voir Fractal / Courbe du dragon
1,264 084 735 306…	Constante de Vardi caractérisant la suite de Sylvester.
1,272727… = 14/11				Approximation simple de la racine carrée du nombre d'or. Écart: 0,0007076…
				Se prête à une fraction continue sympathique; ce qui n'est pas le cas pour Pi seul. C'est aussi le rapport entre la longueur de l'arc d'une cycloïde et la longueur de la ligne droite entre les cuspides. En d’autres termes, lorsque l’essieu d’une roue de rayon r parcourt 2πr, un point de sa jante parcourt 8r, donc le rapport est 8r/2πr = 4/π.
1,277 409 058…	Somme des inverses des nombres octogonaux.
1,282 427 129 1 …	Constante de Glaisher-Kinkelin Apparait dans des sommes et des intégrales de fonctions (gamma, zêta,…) et dans le calcul des hyperfactorielles
		Somme des quatre premières fractions égyptiennes.
					Voir Rêve de deuxième année (Bernoulli)
1,2912987577003… = ln(3)^e					Proche de la constante ci-dessus.

1,3

1,303 577 269 03 ...	Taux d'expansion des commentaires numériques.
	Dimension de Hausdorff des cercles d'Apollonius.
1,30637788386308069046 …	Constante de Mills (Nombres premiers). Le plus petit nombre réel A tel que la partie entière de A^3^n soit un nombre premier, pour tout entier n strictement positif.
= 1,306562964876376527…		Nombre de Cordovan: rapport entre le rayon du cercle circonscrit à l'octogone et son côté.
1,311 028 777 146 059 905 23 …		Constante de la lemniscate L1 (même rôle que pour le cercle).
1,3123 … = 1920/1463		Objet d'une belle identité de Ramanujan.
1,324717957244746026… =		Racine de F(x) = x^3 – x – 1 Nombre de Padovan. Nombre dit " plastique ".
			Factorielle généralisée.

SESQUITIERCE: n + 1/3

Tout nombre augmenté d'un tiers.

Définition: se dit de deux nombres, ou de deux lignes, dont l’une contient l’autre et un tiers de plus.

Latin: sesquitertius, a, um: qui contient une fois et un tiers soit 4/3.

Voir Autres termes en sesqui… / Autres fractions latines

Multimédia

1, 333 … = 4/3 Un des formats des écrans de télévision.

>>>

1,333… = 4/3 = 1 + ¼ + (¼ )^2 + (¼ )^3 + (¼ )^4 + ….			Aire du segment de parabole. Voir Nombre 2 / Progression géométrique Voir Programmation d'un algorithme – Initiation
		Solution de cette équation, en plus et en moins, ainsi que 0. Nombre tel que son cube est égal à lui-même plus sa moitié et son tiers.
1,3541179394…		Fonction gamma de 2/3: fonction factorielle étendue aux nombres non-entiers.
1,372…	Les nombres 2, 5, 17, 37... sont des nombres premiers de la forme n² + 1. On ignore s'ils sont en nombre infini. Conjecture de Hardy et Littlewood: s'ils sont en nombre infini, alors leur nombre jusqu'à x est de l'ordre de q avec C = 1, 372…
1,386294361…	Somme des inverses des nombres hexagonaux.
1,389910664…				Constante utilisée pour tester si un nombre est premier (test de Lucas-Lehmer). Voir Constante de Gottfried Helm

1,4

Multimédia	1,4 fois en moyenne On regarde ses photos 1,4 fois en moyenne.	>>>
Énergie	1,4 tec = 1 tep = 4,2 MWh tep: tonne équivalent pétrole tec: tonne équivalent charbon	>>> Unités

	Forme proche de racine de 2 à 0,0019… près.
	Forme proche de racine de 2 à 0,000018… près.
= 1,414 213 562 373 095 048 801 688 872 420 969 807...	Constante de Pythagore, nombre irrationnel. Mesure de la diagonale du carré de côté 1. Voir développements complets sur les pages Racine de 2 Motif particulier en 14 14 21 35 >>> Base du format du papier A4.
	Forme proche de racine de 2 à 0,000036… près.
1,41428… = 99 / 70	Nombre périodique proche de racine de 2. 1,4142857142857… les mêmes que dans 1/7.
1,42857… = 10 / 7 = 1,42857 142857 142857 ...	Nombre périodique avec nombre têtu. Approximation de racine de 2 en septièmes.

Transport

1,435

Écartement standard des rails de chemin de fer en mètre.

>>>

1,44	Limite de Chandrasekhar.
1,442249… = 3^1/3	Racine cubique de 3.
1,444 667 … = e ^1 / e = 1, 44466 78610 09766 13366 …	Solution de Steiner (1850): valeur pour laquelle la fonction x^1 / x passe par un maximum. La fonction x^x^x^x... (x puissance x, puissance x, etc. jusqu'à l'infini) a une limite si x est compris entre (Euler): e ^-e = 0,065 988 et e ^1/e = 1,444 667. Voir Constante "e" et allure de la courbe
1,45 = 29/20 = 1/2 + 1/3 + 1/4 + 1/5 + 1/6	Somme des inverses des nombres >>>
1,465 571 231 8…	Super nombre d'or.
1,467 078 079 4 …	Constante de Porter Caractérise l'efficacité de l'algorithme d'Euclide.
	Valeur critique pour la décision d'une fourmi descendant un cylindre plein >>>

Suite	Voir le menu en haut de page Nombres de 1,5 à 1,9 Racines – Table
Voir	Débutants – Index Départ de nombreuses suites Nombres – Glossaire Premier nombre géométrique
Cette page	http://villemin.gerard.free.fr/NombDico/UnP2.htm