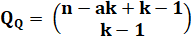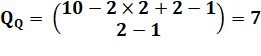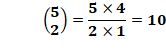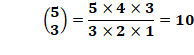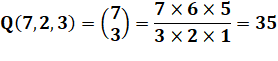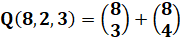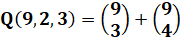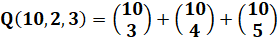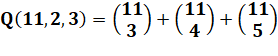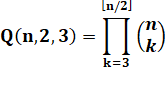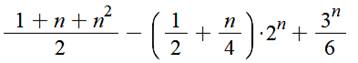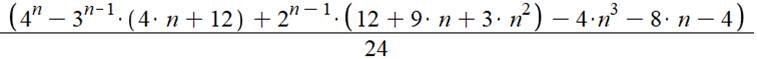|
||||||||||||||||||||||||||||||||||||||||
![]()
|
n balles
numérotées dans k boites quelconques avec minimum de q balles dans
chaque boite
Cas classique : 10
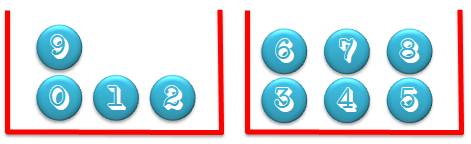
balles dans deux boites avec 2 au minimum dans chaque. Équivalent à: les dix chiffres de 0 à 9 répartis dans deux
ensembles, chacun contenant au moins deux chiffres. On commencera avec des
cas plus simples pour comprendre la façon de compter. |
Anglais: Number of ways of placing n labeled balls into
k indistinguishable boxes with at least q balls in each box
|
|
||
|
Si les
balles ne sont pas numérotées, ni les paniers, on retrouve la formule vue précédemment. |
|
|
|
Si les
balles sont numérotées, la quantité de cas est nettement plus élevée. Voyons comment arriver à ce compte. |
QN = 2n–1 – (n – 1) –
2 QN = 210–1 – (10–1) –
2 = 501 |
|
Notation
|
[n, k, q] pour n balles
numérotées dans k boites avec un minimum de q dans chacune ou n nombres
réparties dans k ensembles avec un minimum de q nombres dans chaque ensemble. [10, 2, 2] pour 10 balles
numérotées dans 2 boites avec un minimum de 2 dans chacune ou 10 nombres
réparties dans 2 ensembles avec un minimum de 2 nombres dans chaque ensemble. |
|
|
||
|
On
considère les nombres 1, 2 et 3. Combien
de possibilités de les partager en deux ensembles avec 2 nombres minium dans
chaque ensemble. Si on choisit [1, 2, 3], on a bien un ensemble de
3 valide, mais l'autre ensemble contient 0 élément. Ce qui n'est pas valide. |
1 et 2 sont dans l'ensemble x 3 est dans l'ensemble o Répartition avec un minimum de 2 par ensemble: impossible. |
|
|
Avec les
nombres: 1, 2, 3 et 4. Il y a
trois possibilités avec trois autres qui s'avèrent être identiques du fait
que l'on peut intervertir les paniers. Si on choisit trois éléments, le second ensemble
n'en contient qu'un, ce qui n'est pas valide. |
Identification de 6 possibilités dont 3 sont
redondantes dans la mesure où les paniers sont quelconques (non numérotés). |
|
|
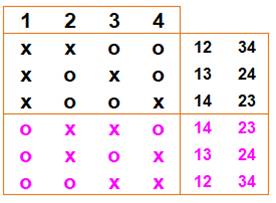
Avec les
nombres: 1, 2, 3, 4 et 5. Il y a
dix possibilités et dix autres qui s'avèrent être identiques. Comme précédemment, impossible de choisir quatre
éléments. Le second ensemble ne contiendrait qu'un seul élément. On constate qu'il s'agit de la demi somme des
combinaisons de:
On ignore les combinaisons de 4 parmi 5 qui ne laisseraient qu'un
élément dans le second ensemble. Une observation aiguisée arrivait à voir que: |
|
|
|
|
||
|
Quantité
de partage des nombres de 1 à n en deux ensembles dont chacun contient au
moins deux éléments. On retrouve la quantité 10 pour n = 5 (m = 4). On a par exemple: 501 possibilités pour tous les
nombres de 0 à 9 (n = 10; m = 9). |
Formule avec
m = n – 1 Q(m, 2, 2) = 2m –
m – 2 Pour m = n – 1 de 4 à 20 3, 10,
25, 56, 119,
246,
501,
1012, 2035, 4082, 8177, 16368, 32751, 65518, 131053, 262124, 524267, … |
|
|
|
|||
|
n = 7 balles à répartir dans 2 paniers avec un minimum de 3
par paniers. Seule possibilité: 3 dans l'un et 4 dans l'autre. |
Choix de 3 parmi 7 pour un panier, le reste dans
l'autre
Vérification Choix de la première balle: 7; Choix de la troisième balle:5; Bilan: 7x6x5 / 6 = 35. |
||
|
n = 8 balles à répartir dans 2 paniers avec un minimum de 3
par paniers. Possibilités:
3/5 et 4/4 |
|
||
|
n = 9 balles à répartir dans 2 paniers avec un minimum de 3
par paniers. Possibilités: 3/6 et 4/5 |
|
||
|
n = 10 balles à répartir dans 2 paniers avec un minimum de 3
par paniers. Possibilités:
3/7; 4/6; 5/5 |
|
||
|
n = 11 balles à répartir dans 2 paniers avec un minimum de 3
par paniers. Possibilités:
3/8; 4/7; 5/6 |
|
||
|
Pour n balles |
|
Quantité pour n de 7 à 25 35,
126, 210, 582, 957, 2431, 4004, 9802, 16263, 39066, 65382, 155210, 261953,
616455, 1048344, 2449614, 4194027, 9740385, 16776890. |
|
|
|
||
|
Répartir
n balles dans 3 paniers avec un
minimum de 2 par paniers. Formule de Vladimir Kruchinin
|
Liste pour n de 6 à 20 15,
105, 490, 1918, 6825, 22935, 74316, 235092, 731731, 2252341, 6879678,
20900922, 63259533, 190957923, 575363776 |
|
|
|
|
|
Répartir n balles dans 4 paniers avec un minimum de 2 par paniers. Formule
Liste pour n de 8 à 20 105,
1260, 9450, 56980, 302995, 1487200, 6914908, 30950920, 134779645, 575156036,
2417578670, 10046531276, 41388056231. |
|
![]()
|
Retour |
||
|
Suite |
||
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
http://villemin.gerard.free.fr/Denombre/aaaBalle/BalleNum.htm |
|
![]()