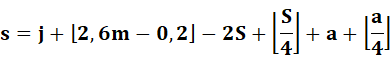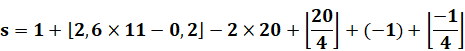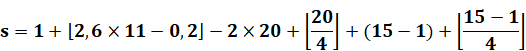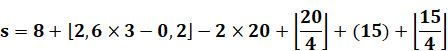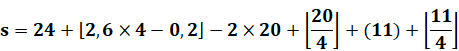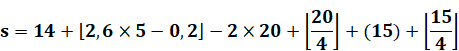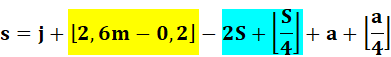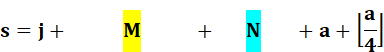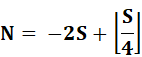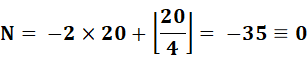NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/03/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	TEMPS
Débutants Général	Mesure du TEMPS DURÉES				Glossaire Temps
INDEX Temps Sciences	Années	Semaine	Jour de la semaine	Jour
		Sommaire de cette page >>> Réponse immédiate sur tableur >>> Méthode avec tabulation >>> Méthode de calcul avec une formule (Gauss) >>> Explication de la formule >>> Bilan

JOUR de la SEMAINE – Calendrier perpétuel

Tabulation ou calcul?

Comment calculer le plus simplement le jour de la semaine pour une date donnée (pour notre calendrier courant, le calendrier grégorien).

Nous avons choisi deux méthodes:

la première, souvent utilisée par les calculateurs prodiges, fait appel à une tabulation que ceux-ci mémorise par cœur; et

la seconde est plus dans l'esprit de ce site car elle met en jeu une formule mathématique que nous expliquerons. Elle permet la programmation simple du calcul. Méthode dite de Gauss.

Anglais: Weekday; to deduce the weekdays; perpetual calendar

Réponse immédiate sur Tableur
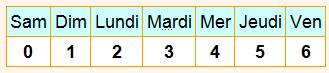
Jour en toutes lettres Le tableur Excel offre la possibilité d'afficher la date avec le jour de la semaine. Pour montrer la procédure, la date est recopiée dans la cellule voisine (C6 = B6). En désignant cette cellule, cliquez le bouton droit et choisissez "format de cellule". Cliquez sur le type montrant le jour de la semaine. Jour codé avec des nombres Pour une réponse numérique, utilisez la fonction: JOURSEM. Voyez l'aide pour connaitre la transcription. Ex: 1 pour dimanche.

Internet fournit des calculateurs en ligne >>>

Calendrier sur Excel

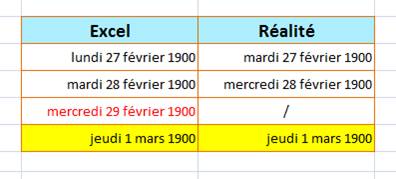
Le tableur Excel est pratique pour manipuler les jours de la semaine depuis l'année 1900 jusqu'à l'an 9999. En fait à partit du 1^er mars 1900. En effet, par erreur, Excel considère que l'année 1900 est bissextile.

MÉTHODE la plus pratique par tabulation
Principe	Exemple
CALCUL EN 3 ÉTAPES + 2 optionnelles
1) Prendre les deux derniers chiffres de l'année		98
Le nombre de douzaines	98 = 8 x 12 + 2 =>	8
Reste de la division par 12		2
Nombres de fois 4 dans le reste	2 = 4 x 0 + 2 =>	0
Ajouter ces trois chiffres	8 + 2 + 0 =	10
Reste de la division par 7 (modulo 7)	10 = 7 x 1 + 3 =>	3
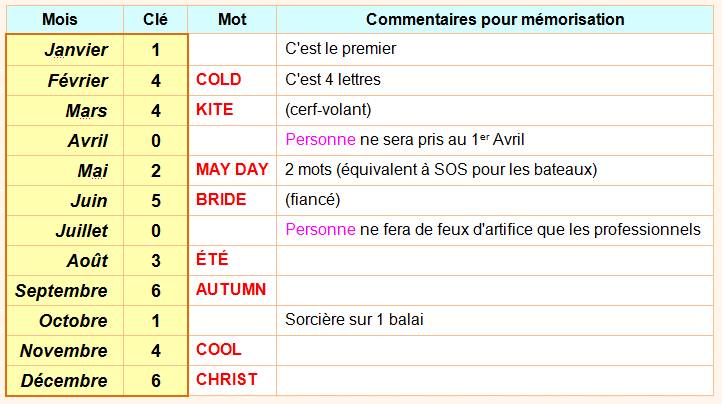
2) Prendre le nombre clé du mois dans la table	Janvier =>	1
Ajouter (modulo 7, si nécessaire)	3 + 1 =	4
3) Ajouter le jour	4 + 11 =	15
Modulo 7	15 = 7 x 2 + 1=>	1
4) Si l'année est bissextile
et pour janvier et février seulement, retrancher 1
5) Si c'est une année en 1900, c'est bien
Si c'est une année en 2000, retrancher 1 Si c'est une année en 1800, ajouter 2
Résultat :		1
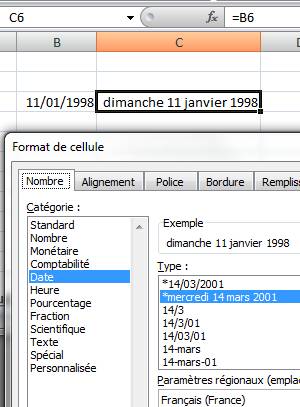
Lire le jour de la semaine dans la table	Dimanche 11 janvier 1998
Table des mois
Une autre façon de mémoriser la table pour les matheux

Voir Mnémotechnique

MÉTHODE de calcul avec la formule de Gauss
Formule de Gauss	mod 7
Calculs	Le résultat du calcul est le reste de la division par 7 de "s" (semaine). C'est ce qu'exprime le "mod 7". Les crochets non fermés en haut mentionnent la fonction plancher (floor). Ex: 3,2 => 3; -0,25 => -1.
Exemple	1^er janvier 2000
Le jour du mois de 1 à 31			j = 1
Le numéro du mois en commençant par mars = 1; avril = 2; … janvier = 11 … Ce compte évite le problème du mois de février.			m = 11
Le numéro du siècle			S = 20
L'année (deux derniers chiffres); sauf pour janvier et février, on prendra l'année – 1.			a = 00 – 1 = – 1
Le jour de la semaine est rendu avec la convention			dimanche = 0, lundi = 1, etc.
Calcul
En mod 7		On ajoute 2 x 7 pour passer en positif.
Correspondance avec dimanche = 0, lundi = 1, etc.		Ce qui correspond à un samedi.

Autres exemples
01/01/2015	(Souvenez-vous, on commence avec 0 pour dimanche) Vendredi
08/05/2015	Vendredi
24/06/2011	Vendredi
14/07/2015	Mardi

Gauss

En 1800, Gauss avait trouvé une formule de ce type indiquant le premier jour de l'an. Son travail manuscrit, non publié, a été intégré à son œuvre en 1927.

La formule indiquée ci-dessus est une généralisation de la méthode de Gauss appliquée à tous les jours de l'année.

Explication de la formule – Principe
Formule toujours en modulo 7
Trois termes (relativement) faciles à comprendre
Progression normale selon la quantité de jours					j mod 7 cycle de la semaine
Une année supplémentaire décale d'un cran le jour de la semaine. Notez que 1^er janvier et 31 décembre tombent le même jour de la semaine.					365 = 52 x 7 + 1 365 mod 7 = 1 d'où la présence de a mod 7
Une année bissextile avec le 29 février décale ce bel ensemble d'un cran supplémentaire					Une fois tous les quatre ans. D’où la recherche de l'entier lors de la division par 4 avec: plancher de a/4.
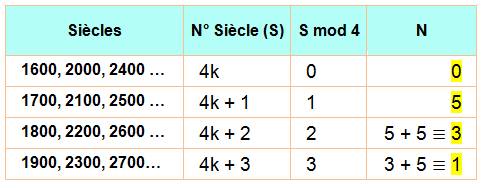
Valeur de N – Effet des années bissextiles au passage des siècles
Décalage due aux 100 ans				100 = 2 mod 7 Deux crans
Quantité d'années bissextiles durant le siècle Décalage correspondant				100 / 4 = 25 25 – 1 = 24 (siècle non bissextile) 24 mod 7 = 3 Trois crans
Effet total de décalage dû aux années bissextiles				2 + 3 = 5 crans / siècle
Effet cyclique sur 400 ans, en prenant les numéros de siècle divisibles par 4 comme origine. Note importante: on pourrait se contenter de mémoriser cette petite table et s'épargner le calcul.
Formulation (recherche empirique)
Exemple pour 2015, numéro du siècle 20 Pour calculer -35 mod 7, ajoutez 5 x 7 = 35, ce qui donne 0.
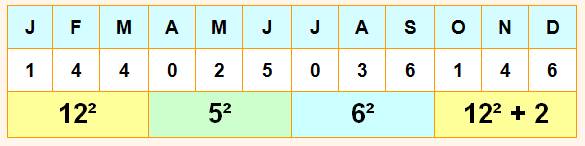
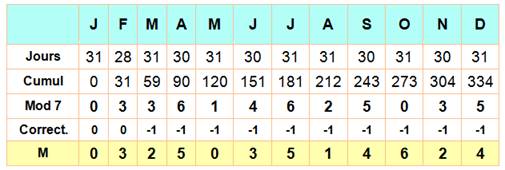
Valeur de M – Effet des mois avec leurs 28, 30 ou 31 jours pour une année normale
Calcul de la quantité de jours écoulés depuis le début de l'année et calcul du modulo 7. Note importante: on pourrait se contenter de mémoriser cette petite table et s'épargner le calcul.	Le décalage (M) dû au compte de jours dans le mois est donné par ce pied de tableau. La correction (0 ou -1) est le fait du comptage des mois à partir de mars.
Formulation (recherche empirique)
Exemple; juillet pour lequel m = 5

Bilan

La première méthode, avec des facilités en calcul mental, une bonne mémoire et de l'entraînement, permet sans doute de faire sensation en calculant les jours de la semaine de tête.

La seconde méthode, avec la formule et les deux tables permet la même prouesse. Cette méthode permet également un calcul systématique par ordinateur.

D'autres méthodes et d'autres formules existent. Je me suis limité à celles-ci qui me semblent les plus significatives.

Suite	Mois Semaine Année et Soleil  Calendriers du monde Mois et lunaisons Saros
Voir	Algorithmes Arc-en-ciel Année 2011 et palindromes Avions Calendrier Cycle de Méton 19 ans Cycle des apsides 8,85 ans Cycle des nœuds 18, 61 ans Dates curieuses et chanceuses … Dates palindromes Dieu et Marcel Électroniques en voiture Heure Jour L'année 0 n'existe pas L'heure de l'insecte Lundi en huit, en quinze … Météorites Millenium Minutes & secondes Montre Montre & Horloge Preuve de la rotation de la Terre Requins Semaine prochaine, lundi en huit … Statistiques Temps - Glossaire Temps de Planck Tour du monde en quatre-vingts jours TP sur les dates avec tableur Vendredi 13
Sites	Quel est le jour de la semaine – ephemeride.com Calendrier – Maths pour tous (Unviversité de Rouen) – Donne le jour de la semaine et explique la formulation mathématique. Trouver le jour de la semaine – Wikipédia – Recense diverses formules Weekdays Calculator – timeanddate – Et toutes sotrtes d'informations realtives aux dates
Cette page	http://villemin.gerard.free.fr/aScience/Unites/Temps/JourSema.htm