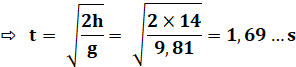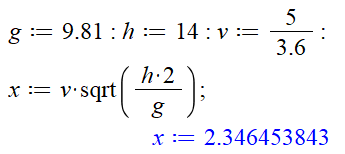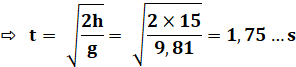|
|||||||||||||||||||||||||||||
![]()
|
Étude du mouvement du plongeur ou d'un projectile Calculs pratiques de la distance de
chute Application des notions vues
à la page projectile. Commentaires sur
l'application d'un tel calcul théorique à la réalité du plongeon. Les formules de base
Pour résoudre ce genre de problème il faut comprendre, comme l'avait
fait Galilée
en son temps, que les mouvements du projectile en horizontal et en vertical
sont indépendants. On peut les calculer séparément et les combiner lorsque
nécessaire. |
|
Source image: Don't
Cliff Jump Like a Dummy—Use Physics
|
|
||
|
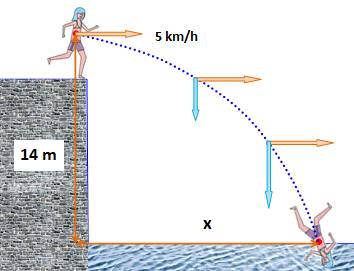
Plongeant
de 14 m (hauteur de son centre de gravité par rapport au niveau de l'eau) à
quelle distance x la plongeuse va t'elle atteindre l'eau ? Elle
arrive au bord avec une vitesse de 5 km/h. |
|
|
|
En
vertical, sans vitesse initiale, elle tomberait dans l'eau en un temps qui se
calcule simplement. La
vitesse initiale en vertical est égale à 0, ce qui élimine le deuxième terme
et permet de calculer t. L'accélération
de la pesanteur (g) est donnée avec la valeur classique 9,81 m/s². |
|
|
|
Pendant
cette chute verticale, la plongeuse se déplace en horizontal sous l'effet de
sa vitesse initiale, laquelle est conservée tout le long de la chute. Il
n'y a pas d'accélération en horizontal (a = 0). La vitesse est convertie en
m/s avec le facteur 3,6. |
|
|
|
|
|
|
Données Un
plongeur de 60 kg prend son élan sur 10 mètres avant de sauter d'une falaise
de 14 mètres de haut. Quelle est la distance du point de chute dans l'eau? Observations
liminaires La
distance doit s'interpréter: distance par rapport à la verticale du point de
départ. Dans la réalité, il faudra compter avec la pente de la falaise. La
trajectoire de la chute est une parabole (la hauteur z est une fonction de la distance au carré:
x²). Le
temps de chute dans le vide ne dépend pas de la masse, mais la chute va
dépendre de la corpulence du corps qui offrira plus ou moins de résistance à
l'air: un peu en vertical et beaucoup plus en horizontal. La
longueur de la course d'élan n'a pas d'effet sauf à donner une certaine
vitesse au moment de la chute. Celle-ci a une grande importance, et elle est
difficile à estimer. La personne va sans doute marquer un certain temps
d'arrêt pour faire son appel et sauter. Son départ se fera sans doute avec un
angle d'envol vers le haut. Exemple de calcul
théorique
(les mêmes chiffres que ci-dessus)
Vitesse
au moment du saut Il
est probable que le mouvement soit très ralenti au moment de l'appel du pied
pour sauter. L'énergie cinétique emmagasinée au cours de la course va sans
doute bénéficier plus à faire l'appel du pied et bondir. Point
de chute au sol La
distance est égale à la vitesse au moment de la chute multipliée par la
racine carrée de 2 fois la hauteur divisée par l'accélération de la pesanteur
g. Avec
nos paramètres, on trouve une chute à 2,34 m du pied de la falaise, si elle
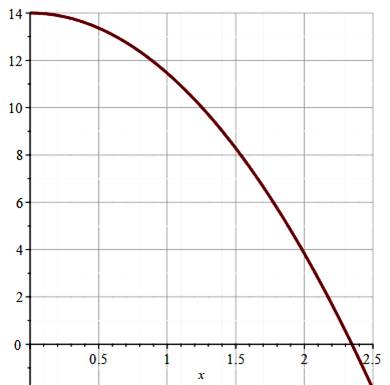
est bien verticale. Courbe
de chute
|
|
|
|
||
|
Même
cas de figure, mais la personne saute en arrivant au bord de la falaise. Hypothèse d'un saut à 1 m de haut qui l'amène à 1
m du bord tout en gardant sa vitesse horizontale à 5 km/h Gain de 1 mètre et 8 cm seulement. |
|
|
La suite tente de donner un calcul plus précis en cas d'angle d'envol.
|
Angle
de saut En
prenant l'appel, le corps monte légèrement. L'angle peut varier de 0° à 45°.
En fait, le calcul montre que l'on ne gagne pas grand-chose en partant avec
un petit angle. Par contre, on perd beaucoup à vouloir faire un appel qui
fait monter haut (grand angle). En plus, la consommation d'énergie pour faire
un saut en hauteur, fait perdre de la vitesse et donc de la distance. L'angle
optimum se situe autour de 15°. Autres
paramètres D'autres
phénomènes peuvent intervenir pour diminuer la distance, comme:
Conclusions
La
hauteur de chute est un facteur primordial pour déterminer la distance de
chute. Si
l'élan permet de sauter légèrement plus loin, il n'est pas sûr que la vitesse
horizontale soit conservée. La
vitesse au moment du saut fait gagner en longueur, mais encore faut-il la
conserver au moment de l'appel. La
distance pour une hauteur de plongée de 14 m est sans doute comprise entre 2
à 3 mètres. Attention: cette distance est mesurée à
l'aplomb du départ de la chute. Le pied est rarement à la verticale. Il faut
tenir compte de la pente de la falaise. Il est hasardeux d'être plus précis. |
|
|
||
|
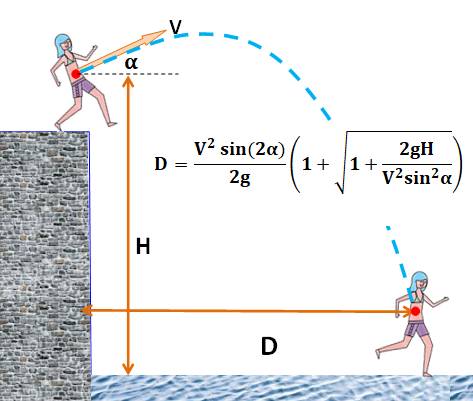
Avec un
angle au départ, la formule est montrée sur la figure. Angle optimal 15°.
Plus grand et D diminue. Avec H = 14 m et angle = 15° Cas d'un individu normal V = 5 km/h (1,4 m/s) Cas plongeur confirmé V = 8 km/h (2,2 m/s) Cas exceptionnel Un athlète de haut niveau peut peut-être atteindre 15 km/h (4 m/s) au
moment du saut. Alors D = 7,25 m. |
|
|
Anglais: The physics of falling from a height / forensic
physics (physique légale)
|
La
chute d'un projectile inerte ne pose pas de problème particulier. Par contre,
les paramètres définissant un plongeur au départ de son saut sont difficiles
à évaluer. Consultez les références indiquées pour en
savoir (peut-être) plus. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Calculateur |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Physique/DYNAMIQ/Plongeur.htm
|