NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/04/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de Nombres
Débutants Premiers	NOMBRES PREMIERS				Glossaire Premiers
INDEX Types de premiers Premiers Nombres	Premier	Sophie Germain	Premier sûr	Premiers de Chen
	Pointés	Luhn	Pierpont
		Sommaire de cette page >>> Approche >>> Nombres premiers pointés par la somme des chiffres >>> Nombres premiers pointés par le produit des chiffres >>> Liste de tels nombres >>> Liste des premiers justes pointés >>> Chaines de premiers pointés >>> Programmation

Nombres premiers POINTÉS

Nombre premier tel que, en lui ajoutant la somme (ou le produit) de ses chiffres, il désigne le nombre premier suivant.

Si la somme (ou le produit) des chiffres pointe vers:

un nombre composé: c'est bien banal;

un nombre premier: c'est un nombre premier pointé ordinaire

le nombre premier suivant: c'est un nombre premier qui pointe juste.

Illustration des situations possibles

Voir Barre magique des nombres premiers

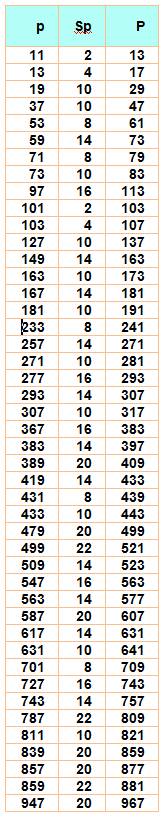
Nombres premiers pointés par la somme des chiffres
Famille	Nombre / Diviseurs / Multiplicatif / Premiers … / Types de nombres premiers et cousins
Définition	NOMBRES PREMIERS POINTÉS par la somme des chiffres Couple de nombres premiers p et P tels que P = p + somme des chiffres de p Ils sont justes pointés si le second est le nombre premier suivant. Nommé: a-pointé.
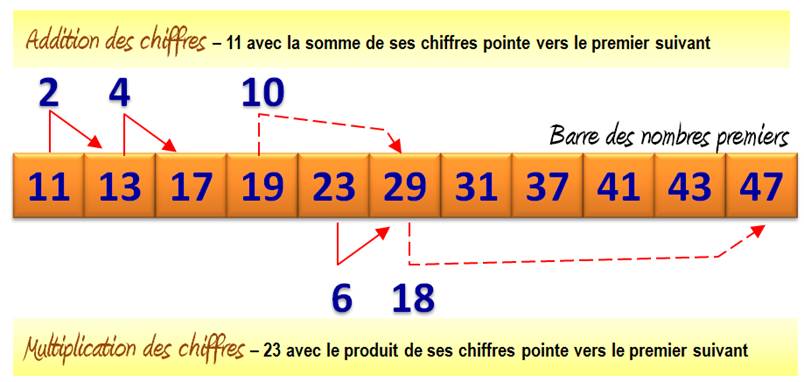
Exemples	11 et 11 + 1 + 1 = 13 13 et 13 + 1 + 3 = 17
Anglais	A prime number  p  is called a-pointer if the next prime number can be obtained adding  p  to its sum of digits (here the 'a' stands for additive).
Auteur	Joseph L. Pe >>>

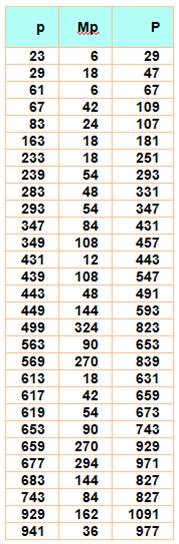
Nombres premiers pointés par le produit des chiffres
Famille	Nombre / Diviseurs / Multiplicatif / Premiers … / Types de nombres premiers et cousins
Définition	NOMBRES PREMIERS POINTÉS par le produit des chiffres Couple de nombres premiers p et P tels que P = p + produit des chiffres de p Ils sont justes pointés si le second est le nombre premier suivant. Nommé: m-pointé.
Exemples	23 et 23 + 2x3 = 29 61 et 61 + 6x1 = 67
Anglais	Primes p such that the next prime after p can be obtained from p by adding the product of the digits of p.
Auteur	Joseph L. Pe >>>

Liste des premiers pointés (ordinaires) jusqu'à 1 000, puis 10 000
La somme ou le produit des chiffres pointe vers un nombre premier (pas nécessairement le suivant).
Additif (45) 228 jusqu'à 10000 81, 233, 257, 271, 277, 293, 307, 367, 383, 389, 419, 431, 433, 479, 499, 509, 547, 563, 587, 617, 631, 701, 727, 743, 787, 811, 839, 857, 859, 947, 1009, 1049, 1061, 1087, 1153, 1171, 1223, 1283, 1409, 1423, 1483, 1489, 1553, 1559, 1579, 1597, 1601, 1607, 1733, 1801, 1847, 1861, 1867, 1933, 1973, 1999, 2017, 2039, 2053, 2129, 2143, 2213, 2237, 2273, 2293, 2341, 2383, 2389, 2521, 2543, 2617, 2633, 2657, 2671, 2677, 2693, 2729, 2767, 2837, 2857, 2903, 3041, 3067, 3089, 3221, 3313, 3373, 3391, 3449, 3469, 3517, 3533, 3539, 3559, 3593, 3607, 3623, 3643, 3719, 3739, 3797, 3889, 3931, 4013, 4057, 4079, 4211, 4217, 4231, 4273, 4493, 4507, 4547, 4583, 4637, 4657, 4729, 4787, 4789, 4877, 4903, 4909, 4967, 5003, 5009, 5087, 5153, 5281, 5333, 5393, 5449, 5483, 5623, 5641, 5647, 5689, 5717, 5779, 5791, 5807, 5827, 5861, 5869, 5881, 6037, 6053, 6073, 6079, 6121, 6211, 6257, 6271, 6277, 6301, 6323, 6343, 6367, 6529, 6547, 6637, 6653, 6703, 6761, 6781, 6857, 6949, 6961, 7027, 7043, 7193, 7333, 7489, 7517, 7537, 7577, 7681, 7937, 8039, 8053, 8059, 8101, 8147, 8273, 8291, 8431, 8521, 8543, 8693, 8699, 8741, 8761, 8837, 8839, 8941, 8969, 9001, 9029, 9043, 9137, 9199, 9241, 9319, 9371, 9377, 9391, 9403, 9421, 9623, 9649, 9689, 9739, 9791, 9829	Multiplicatif (29) 278 jusqu'à 10000 23, 29, 61, 67, 83, 163, 233, 239, 283, 293, 347, 349, 431, 439, 443, 449, 499, 563, 569, 613, 617, 619, 653, 659, 677, 683, 743, 929, 941, 1123, 1163, 1217, 1231, 1237, 1249, 1289, 1297, 1321, 1367, 1423, 1427, 1447, 1451, 1471, 1483, 1489, 1493, 1499, 1523, 1567, 1657, 1669, 1783, 1787, 1789, 1823, 1867, 1877, 1879, 1949, 2111, 2131, 2137, 2239, 2273, 2297, 2351, 2377, 2417, 2441, 2447, 2459, 2467, 2543, 2549, 2579, 2633, 2663, 2683, 2687, 2699, 2741, 2749, 2753, 2777, 2789, 2791, 2819, 2861, 2999, 3163, 3169, 3217, 3253, 3257, 3259, 3271, 3329, 3413, 3433, 3449, 3457, 3461, 3547, 3581, 3583, 3671, 3673, 3691, 3697, 3727, 3767, 3769, 3823, 3833, 3847, 3881, 3947, 3967, 4129, 4157, 4159, 4177, 4211, 4217, 4229, 4241, 4243, 4253, 4271, 4273, 4297, 4339, 4397, 4423, 4463, 4517, 4523, 4547, 4567, 4597, 4643, 4729, 4813, 4889, 4931, 4937, 4957, 5231, 5233, 5273, 5297, 5323, 5381, 5417, 5437, 5441, 5443, 5639, 5651, 5741, 5743, 5843, 5861, 5867, 6113, 6121, 6163, 6173, 6217, 6269, 6287, 6311, 6329, 6361, 6421, 6427, 6451, 6473, 6481, 6521, 6529, 6551, 6563, 6571, 6599, 6637, 6653, 6689, 6761, 6793, 6827, 6857, 6863, 6869, 6871, 6949, 6971, 6977, 6991, 6997, 7229, 7243, 7247, 7297, 7451, 7459, 7477, 7499, 7541, 7547, 7583, 7643, 7649, 7681, 7687, 7691, 7723, 7741, 7789, 7817, 7829, 7853, 7873, 7883, 8123, 8161, 8191, 8219, 8233, 8237, 8269, 8273, 8329, 8353, 8419, 8431, 8447, 8467, 8537, 8539, 8563, 8573, 8597, 8599, 8669, 8837, 8839, 8951, 8963, 8999, 9221, 9227, 9257, 9277, 9349, 9413, 9419, 9431, 9437, 9461, 9463, 9467, 9587, 9629, 9649, 9677, 9689, 9697, 9743, 9767, 9769, 9811, 9817, 9839, 9851, 9857, 9859

Liste des premiers justes pointés
La somme ou le produit des chiffres pointe vers le nombre premier suivant.
Additif (232 jusqu'à 10 000) 11, 13, 101, 103, 181, 293, 631, 701, 811, 1153, 1171, 1409, 1801, 1933, 2017, 2039, 2053, 2143, 2213, 2521, 2633, 3041, 3089, 3221, 3373, 3391, 3469, 3643, 3739, 4057, 4231, 5153, 5281, 5333, 5449, 5623, 5717, 6053, 6121, 6301, 7043, 7333, 8101, 8543, 9241, 10151, 10313, 10463, 10667, 11161, 11321, 11657, 12203, 12241, 12401, 12553, 12601, 13381, 13523, 13633, 13729, 14087, 14177, 14207, 15017, 15107, 15121, 15413, 15473, 17011, 17123, 17761, 18061, 18313, 18461, 18919, 19141, 20129, 20369, 20431, 21023, 21601, 21713, 21803, 22093, 22453, 22501, 22921, 23003, 23117, 23173, 23311, 23719, 24181, 24923, 25423, 25771, 27043, 29311, 29641, 30119, 30203, 30469, 30713, 31019, 31547, 32203, 32401, 33013, 33091, 33301, 33413, 33811, 33941, 35291, 36319, 36353, 36607, 37123, 37253, 37321, 38351, 39521, 39581, 40543, 41117, 41131, 41203, 41243, 41737, 41911, 42307, 43003, 43117, 43207, 43223, 43913, 44071, 44101, 44389, 44657, 45061, 45139, 46703, 46831, 47221, 47317, 48541, 49081, 49957, 50023, 50111, 50207, 50311, 50513, 50599, 50627, 51691, 51871, 52223, 52267, 53381, 53507, 53527, 54001, 54331, 54421, 54601, 54881, 55127, 55291, 56401, 56999, 57529, 58337, 60413, 60703, 61153, 62327, 63113, 63443, 64189, 64303, 66271, 66763, 68611, 70207, 70249, 71039, 71671, 71741, 72139, 72229, 72623, 73433, 73651, 74027, 74531, 75583, 75941, 76261, 76441, 77291, 77813, 79907, 80491, 80963, 81049, 81773, 82051, 82507, 82729, 83117, 83177, 83357, 83663, 84143, 84349, 84761, 85061, 88301, 89021, 89533, 90203, 91163, 91309, 91433, 92153, 92203, 92269, 93503, 99053	Multiplicatif (21jusqu'à 1 000 000) 23, 61, 1123, 1231, 1321, 2111, 2131, 11261, 11621, 12113, 13121, 15121, 19121, 21911, 22511, 27211, 61211, 116113, 131231, 312161, 611113 14 de plus jusqu'à 10 000 000 1111211, 1111213, 1111361, 1112611, 1123151, 1411411, 1612111, 2111411, 2121131, 3112111, 3116111, 3221111, 4121113, 9111341 Remarque: sauf le premier (23), tous les autres nombres comportent le chiffre 1. Est-ce toujours vrai ? Oui, pour tous les nombres testés, mais non-démontré. Voici trois grands spécimens: 9 111 112 411 111 111 111 9 111 121 113 111 111 131 9 131 111 111 121 111 131

Chaines de premiers pointés
Additif avant-arrière La somme des chiffres du premier p pointe à la fois vers le précédent premier et vers le suivant.	Aucune jusqu'à 10 millions.
Multiplicatif avant-arrière Le produit des chiffres du premier p pointe à la fois vers le précédent premier et vers le suivant.	1 117 21 893 3 116 093	1 123 21 911 3 116 111	1 129 21 929 3 116 129
Additif avant-avant La somme des chiffres du premier p pointe vers le premier suivant, la somme duquel pointe aussi vers le suivant. Ils sont 8 jusqu'à 100 000 et 186 jusqu'à 10 millions.	11 101 2 039 15 107 41 117 43 207 50 599 53 507 104 597 … 9 595 253	13 103 2 053 15 121 41 131 43 223 50 627 53 527 104 623 … 9 595 291	17 107 2 063 15 131 41 141 43 237 50 647 53 549 104 639 … 9 595 331
Multiplicatif avant-avant Le produit des chiffres du premier p pointe vers le premier suivant, le produit duquel pointe aussi vers le suivant. Un seul cas jusqu'à 1 milliard.	1 111 211	1 111 213	1 111 219

Programmation
Programme pour les pointés multiplicatifs	Quantité de valeurs en kt et liste des valeurs en L. Boucle de recherche de 1 à 10 000. Si le nombre est premier, il est converti en base 10 pour disposer des chiffres. Les chiffres sont tous multipliés avec l'instruction mul, du premier chiffre en position 1 au dernier en position nops(N). Rappel: l'instruction nops compte la quantité d'éléments dans la liste. Si n ajouté au produit de ses chiffres (S) est égal au premier suivant, alors le mettre dans la liste L et faire plus 1 sur le compteur. En fin de boucle, imprimer la liste L et le compteur k. Pointés additifs Remplacez mul par sum pour avoir les pointés additifs.

Voir Programmation – Index

Voir	Types de nombres premiers – index
Sites	OEIS A089824 – Primes p such that the next prime after p can be obtained from p by adding the sum of the digits of p. OEIS A089823 – Primes p such that the next prime after p can be obtained from p by adding the product of the digits of p. Puzzle 251. Pointer primes – Joseph L. Pe - Carlos Rivera's Prime Puzzles and Problems Connection A-pointer primes – Number aplenty
Cette page	http://villemin.gerard.free.fr/aNombre/TYPMULTI/PremPoin.htm