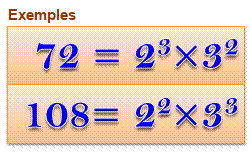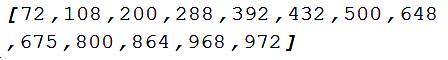|
||||||||||||||||||||||||||||
![]()
|
Nombres d’Achille
Nombres non puissances pures (carrés cubes ou
autres) dont les facteurs sont puissants. |
|
|
||
|
Nombre d’Achille Comme le héros
mythologique Achille, ces nombres sont puissants, mais
pas puissances
parfaites. Nom donné par Henry Bottomley. Nombre dont deux
facteurs
au moins ont des exposants différents (non unité) sans que le nombre soit une
puissance pure. Un nombre
puissant (ou plénipotent), non puissance exacte, est un nombre d’Achille. |
Exemple 72 = 23 x 32 et 72 n’est
pas nk. Liste 72, 108, 200, 288, 392, 432, 500, 648, 675, 800, 864, 968, 972, 1125,
1152, 1323, 1352, 1372, 1568, 1800, 1944, 2000, 2312, 2592, 2700, 2888, 3087,
3200, 3267, 3456, 3528, 3872, 3888, 4000, 4232, 4500, 4563, 4608, 5000, 5292, 5324, 5400, 5408, 5488 ... Plus petits consécutifs |
|
|
Nombre d’Achille
dont le totient
est aussi un nombre d’Achille. 500 = 22 x 53 et
Notez la curiosité avec les exposants inversés. |
Liste 500, 864, 1944, 2000, 2592, 3456, 5000, 10125, 10368, 12348, 12500,
16875, 19652, 19773, 30375, 31104, 32000, 33275, 37044, 40500, 49392, 50000,
52488, 55296, 61731, 64827, 67500, 69984, 78608, 80000, 81000, 83349, 84375,
93312, 108000, ... |
|
|
|
Commentaires Suite de trois programmes pour trouver les nombres d’Achille pour n de
2 à 1000, par exemple. La fonction recherche des exposants des facteurs du nombre n a déjà
été expliquée. La fonction nombre d’Achille test trois propriétés pour décréter que n
est un nombre d’Achille (A = 1) :
Le programme de recherche explore les nombres n de 2 à 1000 et
enregistre les nombres d’Achille (A = 1) dans la liste L (append). En bas, le résultat des traitements. |
Anglais Achilles number : powerful but not perfect power
Voir
Base de la programmation Maxima
Voir
Programmation
– Index y compris les programmes Maxima
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()