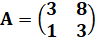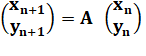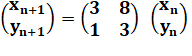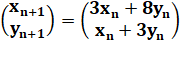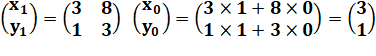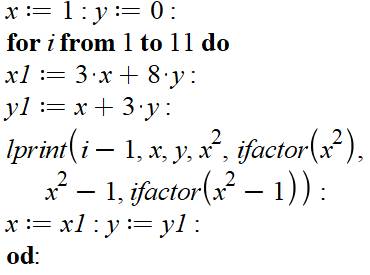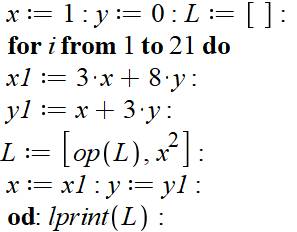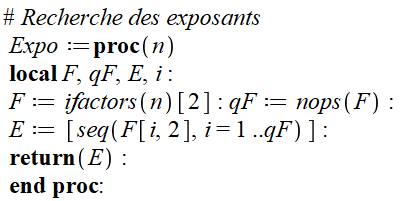|
||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES PUISSANTS JUMEAUX Recherche des nombres consécutifs
simultanément puissants.
D’abord comme corrigé d’un exercice du baccalauréat 2018, puis recherche par programmation. |
|
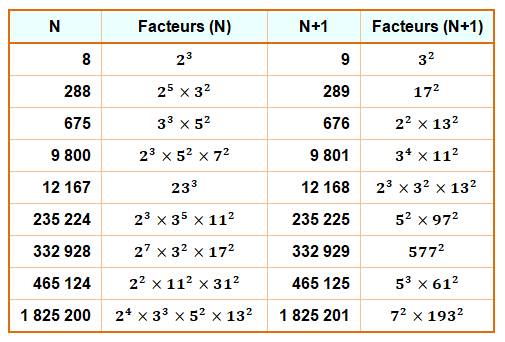
Puissants jumeaux Couple de nombres successifs tous deux puissants:
dont les facteurs sont tous à une puissance supérieure à 1. Tableau des premières occurrences
=> |
|
||
|
Liste des nombres
de tête |
8, 288, 675, 9800, 12167,
235224, 332928, 465124, 1825200, 11309768, 384199200, 592192224, 4931691075,
5425069447, 13051463048, 221322261600, 443365544448, 865363202000,
8192480787000, 11968683934831, 13325427460800, 15061377048200, 28821995554247,
… |
||
|
|
But Identifier les nombres puissants jumeaux et
énoncer les facteurs. Commentaire Procédure Puis qui délivre t = 1 si le nombre est
puissant. Le nombre est présenté sous la forme d'une liste
comprenant les paires: base et exposant de chaque facteur. Si l'exposant (indice 2) est inférieur à 2; le
témoin t de puissance est mis à zéro. Le programme principal analyse les nombres n de 1 à 1000. Calcul des facteurs et interrogation de la procédure. Si les deux témoins de n et n+1 sont à 1, les
deux nombres sont puissants-jumeaux. Impression de la liste L (di simple fait du
poin-virgule). |
||
Voir Programmation – Index
Baccalauréat S 2018
|
Une pétition très suivie a été émise protestant contre la
difficulté du quatrième exercice, jugé infaisable, et contre le troisième
considéré comme hors-programme. Cet exercice "n°4 - Spécialité" a semblé trop abstrait
et, surtout, comportant des notions telles que la ligne brisée jugées hors
programme. |
Baccalauréat S Session 2018 Mathématiques Spécialité Exercice n°4 |
Voir Enseignement
– Index
![]()
|
|
|||
|
On
considère l’équation
suivante dont les inconnues x et y sont des entiers naturels : x² – 8y²
= 1 (E) 1)
Déterminer un couple solution (x ; y) où x et y sont deux entiers
naturels. |
Ne pas hésiter à
prendre y = 0 en premier ; alors ; x = 1 convient, et : (x ;
y) = (1 ; 0) |
||
|
2) On
considère la matrice
On
définit les suites d’entiers naturels (xn) et (yn)
par : x0
= 1 et y0 = 0 et pour
les entiers naturels n :
2a) Démontrer par récurrence
que pour tout entier naturel n, le couple (xn ; yn)
est solution de l’équation E. |
Produit avec matrice
Ce qui donne
Ou encore
|
||
|
Pour n = 1 Propriété
vérifiée (initialisation de la démo par récurrence) |
(égal circonflexe veut dire : correspond à) |
||
|
Supposons la
relation vraie pour n et calculons pour n + 1 (hérédité) |
|
||
|
Développement Qui conduit à 1
en reportant notre hypothèse |
|
||
|
Initialisation + hérédité |
Le couple (xn ; yn)
est bien solution de l’équation E quel que soit n à partir de 0. |
||
|
2b) En
admettant que la suite (xn) est à valeurs strictement positives,
démontrer que pour tout entier naturel n, on a xn+1 > xn. |
Calcul de l’accroissement en x en fonction de x
et y. Les valeurs de x étant positives, il faut sans
doute montrer que c’est vrai pour y. |
|
Valeur de la
différence |
|
|
Avec xn
positif, reste à montrer que yn est positif La récurrence montre
que l’on ajoute systématiquement une valeur positive : yn+1 est
positif et, entraine que xn+1 l’est aussi. |
y0 = 0
|
|
3) En
déduire que l’équation (E) admet une infinité de couples de solutions |
|
|
Tous les couples
obtenus par cette récurrence sont solutions. La suite xn est
strictement croissante. Alors : |
Il y a une infinité de solutions. |
|
|
|||
|
Un entier
naturel n est appelé un nombre puissant
lorsque, pour tout diviseur premier p de n, p² divise n. 1) Vérifier qu’il existe deux
nombres entiers consécutifs inférieurs à 10 qui sont puissants. L’objectif de cette partie est de démontrer, à
l’aide des résultats de la partie A, qu’il existe une infinité de couples de
nombres entiers naturels consécutifs puissants et d’en trouver quelques
exemples. |
1, 2, 3 non 4 = 2² oui 5 non 6 = 2x 3 non 7 non 8 = 2 x 2² oui 9 = 3² oui Voir Liste
des nombres puissants (4,
8, 9, 16, 25, 27, 32, 36, 49, …) |
||
|
Soit a et
b deux entiers naturels. Montrer
que l’entier naturel n = a2b3 est un nombre puissant. |
Les exposants des facteurs
premiers des nombres puissants sont égaux ou supérieurs à 2. |
||
|
Les nombre a et
b se décomposent en facteurs premiers (théorème fondamental
de l'arithmétique |
a2 = p12 . p22
. p32 … b3 = q13 . q23
. q33 … |
||
|
Tous les
facteurs en |
pi2 sont évidemment divisibles par pi2 qj3 = qj2 . qj sont
divisibles par qj2 |
||
|
Les nombres en n
= a2b3 |
Sont divisibles par le carré
de tous leurs facteurs premiers, ils sont puissants. |
||
|
3)
Montrer que si (x ; y) est un couple solution de l’équation (E) définie
dans la partie A, alors x² – 1 et x² sont des entiers consécutifs puissants. |
Équation x² – 8y² = 1 (E) Solutions (x0 ; y0) = (1 ; 0) et
|
|
|
xn
est puissant : |
|
|
|
xn+1
est puissant : |
Puissant si:
|
|
|
4)
Conclure quant à l’objectif fixé pour cette partie, en démontrant qu’il
existe une infinité de couples de nombres entiers consécutifs puissants. Déterminer
deux nombres entiers consécutifs puissants supérieurs à 2018. |
On a déjà montré qu’il y a une infinité de solutions en xn. |
|||||||||||||||||||||||||||||||||||||||||||
|
On vient de
démontrer que si (x ; y) est un couple solution, il satisfait l’équation
E |
Alors, il existe une infinité de nombres x² et x² - 1 solution |
|||||||||||||||||||||||||||||||||||||||||||
|
Couple puissant
supérieur à 2018 |
(9 800; 9 801) |
|||||||||||||||||||||||||||||||||||||||||||
|
Tableau de calcul de xn et yn avec la définition donnée en partie
A : x := 3x + 8y y := x + 3y |
|
|||||||||||||||||||||||||||||||||||||||||||
![]()
|
|
||
|
|
Commentaires Initialisation des valeurs de x et y. Lancement de la boucle d’exploration en i. Calcul des nouvelles valeurs de x et y en
fonction des anciennes. Impression des valeurs désirées (Voir le tableau ci-dessous). Mise à jour des valeurs de x et y. Opération
indispensable pour x, car l’ancienne valeur de x est utilisée pour calculer
la nouvelle valeur de y. Fin de boucle avec do à l’envers. |
|
Tableau issu
du programme ci-dessus après mise en forme
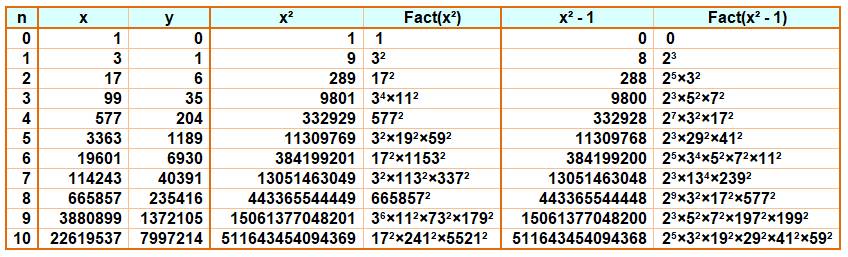
|
Programme poduisant x²
|
Valeurs de la liste des x² successifs jusqu’à 20
nombres 1, 9, 289, 9801, 332929, 11309769, 384199201, 13051463049,
443365544449, 15061377048201, 511643454094369, 17380816062160329,
590436102659356801, 20057446674355970889, 681362750825443653409,
23146276081390728245001, 786292024016459316676609,
26710782540478226038759689, 907380314352243226001152801,
30824219905435791458000435529, 1047116096470464666346013655169 |
|
|
||
|
|
Commentaires Sous-programme de recherche
des exposants des facteurs de n : Expo(n). Dans F, on place le deuxième terme des facteurs
obtenus avec ifactors (une particularité
de Maple). Création d’une liste qui énumère les exposants
des facteurs (le deuxième élément du ième facteur). Sous-programme de détection
d’un nombre puissant P= 1 si puissant). Ne reçoit les exposants des facteurs de n. P est mis à 1 et sera descendu à 0 si l’un des
exposants est inférieur à 2. Programme principal de
recherche des nombres puissants consécutifs. Boucle de recherche sur n. Pour chacun, test si lui et son successeur son
puissants. Si oui, le nombre le plus grand est ajouté à la
liste qui sera imprimée. Résultats Ce programme de recherche exhaustif montre la
formule indiquée ci-dessus identifie des nombres doublement puissants, mais
pas tous. Par exemple 676 = 22.13. et
675 = 33.52 Liste (en rouge, les nouveaux) 9, 289, 676,
9 801, 12 168, 235 225, 332 929, 465
125, 1 825 201 … |
|
|
Suite |
Voir haut
de page |
|
Voir |
|
|
Site |
|
|
Cette page |