|
||||||||||||||||||||||||||||||||||||||||||||
![]()
|
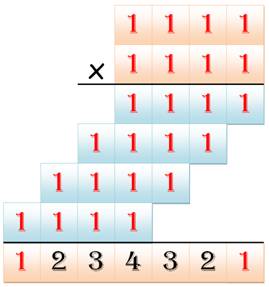
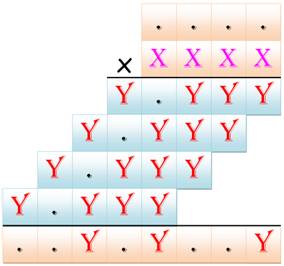
Multiplication à 4 x 4
chiffres Multiplications à quatre chiffres par quatre
chiffres. On se propose de trouver quelles sont les multiplications de ce type
qui présentent le maximum de chiffres identiques, y compris dans les produits
intermédiaires. |
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
9999,
9991, 9999, 89991, 89991, 89991, 99900009, 24 9999,
9999, 89991, 89991, 89991, 89991, 99980001, 23
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()