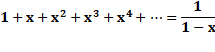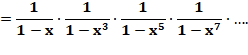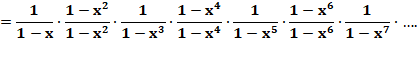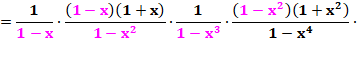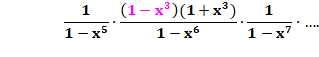NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 28/10/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Partitions
Débutants Algèbre	Fonctions GÉNÉRATRICES				Glossaire Partition
INDEX Suites Partition	Introduction	Nombres entiers	Diviseurs	Principales FG
		Partitions	K termes	Distincts = Impairs
		Sommaire de cette page >>> Quelques partitions en exemples >>> Quantité de partitions distinctes ou impaires >>> Partitions particulières >>> Démonstration du théorème

Quantité de PARTITIONS

Qté DISTINCTS = Qté IMPAIRS

Extraordinaire ! Il y a autant de partitions en nombres distincts (partitions strictes) que de partitions en nombres impairs (odd en anglais):

QD(n) = QI(n) autre notation: p^d(n) = p^o(n)

Les fonctions génératrices sont appelées pour réaliser le démonstration.

Cette propriété exceptionnelle a été trouvée par Euler.

Voir Partitions strictes et partitions impaires – Approche et programmation

Quelques partitions
Partitions avec	des nombres IMPAIRS	des nombres DISTINCTS
Définition	Les termes de la partition ne sont que des nombres impairs, même répétés.	Les termes de la partition sont tous différents (donc non répétés).
Nombre 7 5 partitions dans les deux cas	[1, 1, 1, 1, 1, 1, 1] [1, 1, 1, 1, 3] [1, 3, 3] [1, 1, 5] [7]	[1, 2, 4] [3, 4] [2, 5] [1, 6] [7]
Nombre 8 6 partitions dans les deux cas	[1, 1, 1, 1, 1, 1, 1, 1] [1, 1, 1, 1, 1, 3] [1, 1, 3, 3] [1, 1, 1, 5] [3, 5] [1, 7	[1, 3, 4] [1, 2, 5] [3, 5] [2, 6] [1, 7] [8]
Nombre 11 12 partitions dans les deux cas	[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] [1, 1, 1, 1, 1, 1, 1, 1, 3] [1, 1, 1, 1, 1, 3, 3] [1, 1, 3, 3, 3] [1, 1, 1, 1, 1, 1, 5] [1, 1, 1, 3, 5] [3, 3, 5] [1, 5, 5] [1, 1, 1, 1, 7] [1, 3, 7] [1, 1, 9] [11]	[1, 2, 3, 5] [2, 4, 5] [2, 3, 6] [1, 4, 6] [5, 6] [1, 3, 7] [4, 7] [1, 2, 8] [3, 8] [2, 9] [1, 10] [11]

Voir Table des partitions distinctes

Quantité de partitions distinctes ou impaires des nombres n de 1 à 30

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
1	1	2	2	3	4	5	6	8	10	12	15	18	22	27	32	38

18	19	20	21	22	23	24	25	26	27	28	29	30
46	54	64	76	89	104	122	142	165	192	222	256	296

Liste des quantités de partitions jusqu'à n = 120 (en rouge valeur pour les multiples de 10)

1, 1, 2, 2, 3, 4, 5, 6, 8, 10, 12, 15, 18, 22, 27, 32, 38, 46, 54, 64, 76, 89, 104, 122, 142, 165, 192, 222, 256, 296, 340, 390, 448, 512, 585, 668, 760, 864, 982, 1113, 1260, 1426, 1610, 1816, 2048, 2304, 2590, 2910, 3264, 3658, 4097, 4582, 5120, 5718, 6378, 7108, 7917, 8808, 9792, 10880, 12076, 13394, 14848, 16444, 18200, 20132, 22250, 24576, 27130, 29927, 32992, 36352, 40026, 44046, 48446, 53250, 58499, 64234, 70488, 77312, 84756, 92864, 101698, 111322, 121792, 133184, 145578, 159046, 173682, 189586, 206848, 225585, 245920, 267968, 291874, 317788, 345856, 376256, 409174, 444793, 483330, 525016, 570078, 618784, 671418, 728260, 789640, 855906, 927406, 1004544, 1087744, 1177438, 1274118, 1378304, 1490528, 1611388, 1741521, 1881578, 2032290, 2194432, ….

Suite jusqu'à n = 5000

Partitions particulières
Avec que des "1" Il n'existe qu'une partition du nombre n avec que des "1". C'est la somme 1 + 1 + 1 + … + 1 avec n fois le nombre 1.	1x^0 + 1x^1 + 1x^2 + 1x^3 + 1x^4 + … Chaque coefficient indique la quantité de partitions du nombre mis en exposant. On simplifie:
Avec que des "2" C'est la même chose: qu'une seule présentation pour chaque nombre, à condition qu'il soit pair: Ex: 6 = 2 + 2 + 2	1x^0 + 0x^1 + 1x^2 + 0x^3 + 1x^4 + … Chaque coefficient indique la quantité de partitions du nombre mis en exposant. On simplifie:
Avec que des "k" C'est le même principe	1 + x^k + x^2k + x^3k …
Avec que des "1" et des "2" C'est le produit des deux polynômes. Ex: pour le nombre 4, il existe trois partitions avec "1" et "2". Ce sont: 4 = 1+1+1+1 = 1+1+2 = 2 + 2.	(1 + x + x^2 + x^3 + x^4 + … ) . (1 + x^2 + x^4 + x^6 … ) = 1 + x + 2x^2 + 2x^3 + 3x^4 + 3x^5+ …
Avec que des nombres impairs C'est le produit des deux polynômes de rang impair.	(1 + x + …) (1 + x^3 +…) (1 + x^5 +…) …
Avec que des nombres distincts La contribution de chaque nombre à la partition d'un nombre n est nulle ou unique.	(1 + x) (1 + x^2) (1 + x^3) (1 + x^4) … Chaque binôme indique la contribution du nombre en exposant.

Voir Brève 518

Démonstration du théorème
Théorème Pour tout nombre entier, la quantité de partitions distinctes est égale à celle des partitions en nombres impairs.		QD(n) = QI(n) ou (avec o pour odd, impair en anglais) p^d(n) = p^o(n)
Mise en évidence de QD(n) Prenons ce produit infini En le développant	Les coefficients sont égaux aux QD(n)
Mise en évidence de QI(n) Prenons ce produit infini En le développant	Les coefficients sont égaux aux QI(n) Les mêmes que QD(n)
Rappel pour x < 1
Preuve de l'égalité Reprise de l'expression pour Qi(n). On intercale des fractions unité avec puissances paires. Puis expansion des numérateurs Après simplification, les dénominateurs sont éliminés et on retrouve l'expression de QD(n) CQFD.

Suite	Partitions – Quantité fonction du nombre de sommants Fonctions génératrices – Nombres entiers Tables des FG classiques
Voir	Diviseurs – Introduction Diviseurs – Théorie Suites Fractales
Sites	OEIS A000009 - Expansion of Product_{m >= 1} (1 + x^m); number of partitions of n into distinct parts; number of partitions of n into odd parts Euler Gem: Distinct versus Odd Partitions (Tanton Mathematics) – Video Partition Function - Sarbajit Mazumdar, Jyotishka Ray Choudhury (Mettre tout ce texte dans la fen^tre de recherche)
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Suite/FoncDiIm.htm