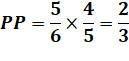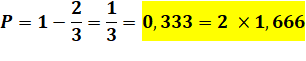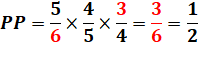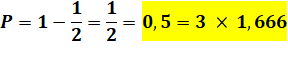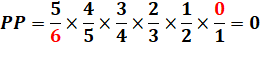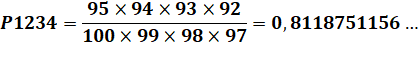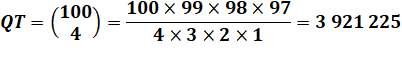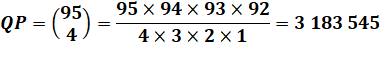|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
LOTO en groupe ou achats de plusieurs tickets Quelle est la probabilité
de gagner en groupe? Soit à plusieurs joueurs, soit en achetant plusieurs
tickets pour le même tirage. Avec k tickets ayant des numéros différents, on a k fois plus de chance
de gagner le gros lot. C'est vrai, et ça vous semble sans doute évident, et
pourtant, pas si sûr! |
Anglais: buying
multiple lottery tickets /
Customers are trying to improve their odds by buying
multiple tickets
|
|
||
|
Jeu de dés
à six faces |
Je mise sur un numéro entre 1 et 6 et je lance un
dé à 6 faces. Je gagne si le numéro du dé correspond à mon numéro. La probabilité de gagner est P = 1/6. Celle de perdre est PP = 5/6 |
|
|
Loterie
avec grille de 100 cases |
Chacun coche un numéro sur une grille. La société des jeux tire une boule parmi 100
boules numérotées de 1 à 100 dans une urne. Je gagne si la boule montre mon numéro. La probabilité de gagner est P
= 1/100. |
|
|
Jeu de
dés à 100 faces |
Ce jeu est équivalent à celui décrit pour la
loterie à 100 cases. Chaque boule de l'urne correspond à une face du
dé. |
|
|
Loto à 49
boules |
Je choisi 6 boules parmi 49. Je gagne si ma combinaison sort parmi 13 983 816. Imaginons un immense dé à 13 983 816 faces. Je gagne si la combinaison tirée correspond à la
mienne. On pourrait penser également à une
grande urne dans laquelle, au lieu des 49 boules, on aurait 13 983 816
boules chacune marquée d'une combinaison de 6 des 49 nombres. |
|
|
Bilan |
Pour comprendre ce qui se passe au Loto, je peux raisonner
sur un dé à 6 faces et généraliser à 13 983 816 faces. Attention, il s'agit d'un
seul dé. Ne pas raisonner avec plusieurs dés, car les numéros seraient
redondants. |
|
|
|
||||||||||||||||||||||||||||||
|
Principe |
Je mise sur un numéro entre 1 et 6 et je lance un
dé à 6 faces. La probabilité d'avoir choisi le numéro donné par
le dé est P = 1/6 = 0,166. |
|||||||||||||||||||||||||||||
|
Deux joueurs |
Deux cas se présentent:
|
|||||||||||||||||||||||||||||
|
Deux joueurs quelconques |
Configurations typiques (selon le
tableau): Colonne 11: le premier joueur joue le 1 et le
second le 1 également. Le tirage donne 6. Ni l'un ni l'autre ne gagne. Pour
les deux c'est perdu (P). Comptez les cas de ce type (un tableur peut faire
l'affaire), vous trouverez 25. Soit 25 cas sur 36. Colonne 16: les deux joueurs jouent séparément le
1 et le 6. Il y a un gagnant lorsque le 6 sort. Il existe 10 cas de cette
sorte (5 pour l'un et 5 pour l'autre). Probabilité: 10/36. Colonne 66: les deux jouent le 6 et c'est le 6
qui sort. Il existe un seul cas de ce type où les deux gagnent. Notez que
s'il s'agit du Loto, le gain est partagé.
Explications La probabilité de gagner de deux joueurs
indépendants est P = 11/36 avec une probabilité de 1/36 qu'ils aient à se partager
le gain au cas où ils auraient gagné tous les deux. Calcul Probabilité de perdre pour chacun: 5/6 Probabilité de perdre pour les deux réunis:
(5/6)² Probabilité de gain pour les deux: P2 = 1 – (5/6)² = 11/36 Généralisation Il est clair que six joueurs, jouant chacun dans
son coin, n'ont pas la certitude de gagner le gros lot! Pas plus que 10 ou 20
joueurs P2 = 1 –
(5/6)2 = 0,305 P6 = 1 –
(5/6)6 = 0,665 P10 = 1 – (5/6)10 = 0,838 P20 = 1 – (5/6)20 = 0,974 |
|||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
Principe |
Dans ce cas qui nous intéresse particulièrement,
les deux joueurs sont de connivence et
évitent de jouer les mêmes numéros. Cas du jeu en
groupe ou en syndicat comme disent les anglo-saxons Même cas de figure: je peux décider de ne pas
partager et de jouer les deux configurations pour mon propre compte. |
|||||||||||||||||||||||||
|
Deux joueurs de connivence |
Configuration typique selon le
tableau: Premier constat à faire, et c'est la clé du calcul:
on ne joue jamais les mêmes numéros. On élimine
donc 6 combinaisons. Sur 36, il en reste 30. Colonne 12: le premier joueur joue le 1 et le
second le 2. Le tirage donne 6.. Pour les deux c'est
perdu (P). Il existe 20 de ce type cas sur 30. Colonne 16: les deux joueurs jouent le 1 et le 6.
Il y a un gagnant. Il existe 10 cas de cette sorte. Probabilité: 10/30. Colonne 55: les deux joueraient leur nombre
fétiche, le 5; mais c'est interdit. Les numéros doivent être différents.
Explications Si deux personnes jouent de connivence sur deux numéros
différents, on élimine les doublons du décompte des jeux possibles: 11, 22,
33, 44, 55 et 66 ne seront pas joués. Le total des cas possibles est donc: 36
– 6 = 30. On retrouve les cas de gain unique avec joueurs
quelconques (10) et la probabilité de gain à deux devient: P2 = 10/30 = 1/3 =
0,333 contre 0,305 dans le cas de deux joueurs quelconque. La concertation augmente les chances de gain (un
peu!) Mais, observation plus importante: La
probabilité est rigoureusement égale à 2 fois la probabilité de gagner seul
(2 x 1/6 = 1/3). Calcul Ayant choisi, un numéro sur 6, il en reste
seulement 5 pour le second. En effet, le second joueur ne joue pas le n° du
premier, mais joue au hasard sur les 5 numéros qui restent. On calcule la probabilité (PP) que les deux
soient perdants: 5 cas sur 6 pour l'un et 4 cas sur 5 pour l'autre. Les deux
événements s'enchainent. Le principe
multiplicatif s'applique.
On retrouve bien deux fois plus de chances avec
deux jeux qu'avec un seul. |
|||||||||||||||||||||||||
|
Trois joueurs de connivence |
PP est une fraction
simple, car avec les simplifications, on obtient le numérateur 3 final (comme
3 joueurs) et le dénominateur 6 (total) initial. |
|||||||||||||||||||||||||
|
Six joueurs de connivence |
On retrouve une probabilité de 100% de gagner en
misant sur chacun des numéros. |
|||||||||||||||||||||||||
Un immense dé avec
une face par combinaison ou alors, toutes les combinaisons dans une urne

|
Au
Loto pour le même tirage, si on achète k tickets avec des combinaisons différentes, la probabilité de gagner est multipliée exactement par k. Attention, les
gains sont à partager si un autre joueur se trouve avoir joué les mêmes
combinaisons que vous. Toutes les mises Il
est évident qu'en misant sur les 13 983 816 combinaisons à la fois, la
combinaison gagnante figurera parmi celles misées. Faisant cela, vous auriez
deux problèmes: 1)
il faudra partager les gains avec tous ceux qui auront misés sur les mêmes
numéros gagnants; et 2)
plus grave, vous aurez payé beaucoup plus que la somme gagnée (le retour au
Loto est estimé à 68%). Voir Miser
toute sa vie Le numéro chance (powerball en
anglais) L'introduction
d'une balle particulière dans le tirage du Loto ne change pas les
conclusions. On peut multiplier par 10, la probabilité de gagner le gros lot
en jouant tous les numéros chance. |
![]()
|
|
||
|
La
tombola met 100 tickets en vente dont un seul est gagnant. |
Cette fois il n'y a pas de tirage; le billet
gagnant est inscrit à l'avance. |
|
|
Achat d'un billet. |
P = 1/100 |
|
|
Achat de 2 billets Ce que
l'on croit à tort. |
P = 2/100 = 0,02 |
|
|
La véritable probabilité La
subtilité: il y a forcément un ticket perdant parmi les deux achtés. On écarte
cette possibilité, il en reste 99. Donc 1
chance sur 99 de gagner. |
P = 1/99 = 0,0101 |
|
|
|
|||
|
Tombola |
100 billets avec cinq billets gagnants. On achète quatre billets parmi les 100 disponibles Quelle est la probabilité
d'avoir au moins un billet gagnant? |
||
|
Calcul de probabilité pour cette tombola |
|||
|
Probabilité de prendre un
billet perdant: |
P1 = 95/100 95, car il y a 5 billets gagnants (le 5 de
l'énoncé est ici). |
||
|
Une fois cela fait,
probabilité d'avoir un second billet perdant: |
P2 = 94/99 94, car 95 moins le premier billet choisi. |
||
|
En cumulant: probabilité que
les deux premiers soient perdants: |
P12 = 95/100 x 94/99 = 0,9020… |
||
|
En poursuivant, probabilité
de quatre perdants: |
(le 4 de l'énoncé est ici). |
||
|
Probabilité d'avoir un
billet gagnant parmi ces quatre billets: |
|
||
|
Calcul combinatoire - Autre méthode de calcul |
|||
|
Quantité de combinaisons
de quatre billets parmi 100: |
|
||
|
Quantité avec aucun billet
gagnant: |
|
||
|
Quantité ayant au moins un
gagnant: |
|
||
|
Probabilité d'un billet
gagnant, au moins: |
|
||
|
Variante |
Cinquante billets sont déjà
vendus sur les 100. On achète deux billets parmi
les 50 restants. |
||
|
Probabilité avec achat d'un
billet: |
Le gagnant est dans les
vendus ou dans l'un des 50 restants, soit 51 possibilités: P = 1 / 51 = 0,019607 |
||
|
Probabilité avec achat de
deux billets. Elle n'est pas doublée! |
Les deux gagnants sont dans
les vendus ou dans l'un des 50 restants, soit 52 possibilités: P = 2 / 52 = 0,038461 < 2 x 0,019230 = 0,039215 |
||
Conclusion selon la presse américaine
Là-bas
la probabilité de gagner le gros lot est 1/ 292 millions
|
En multipliant vos chances
par 10 ou même par 100 en achetant ces quantités de tickets, la probabilité
de gagner au loto reste ridiculement faible, si incroyablement faible que
c'est juste 10 ou 100 fois une perte d'argent. – d'après Wasserstein Même avec 100 tickets,
vous avez encore trois fois plus de chances de vous faire tuer par un éclair
dans l'année et, environ 300 fois plus de probabilités de vous tuer dans un
accident de voiture. Jouer au Loto vous donne cependant le droit de rêver un
peu à "peu de frais" – d'après George Loewenstein
|
Merci à David L. pour cette idée de page
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
Peu
de choses sur Internet concernant le sujet multi-joueurs.
|
|
Cette page |
![]()