|
Édition du: 02/10/2022 |
Faites un double-clic pour un retour en haut de page
![]()
|
NOMBRES 3-adiques Triadiques et leurs représentations Nombres
p-adiques en base 3. Exemple de représentations. Valable
pour les autres p-adiques, mais de plus en plus compliqué à visualiser. En fait, l'exemple
des triadiques permet de se familiariser avec ces nombres étranges. |
||
|
|
Sommaire de cette page >>> Représentation des nombres >>> Construction des ensembles de nombres >>> Triadiques – Représentation par ensembles >>> Triadiques – Représentation par arbre >>> Triadiques – Représentation par puits
fractals |
Débutants Glossaire |
|
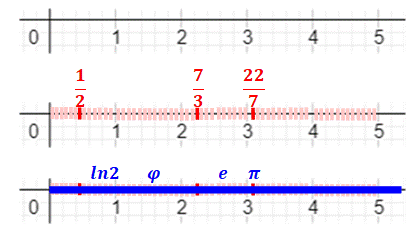
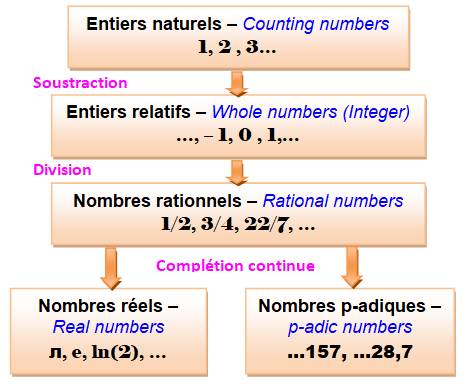
Les
nombres entiers
ont représentés par des points espacés régulièrement sur une droite. Les
nombres rationnels
(fractions) complète ces points Les
nombres réels
remplissent la droite des nombres de manière continue. |
Droite des nombres
"ordinaires"
|
|
|
Comment
représenter les nombres p-adiques ? La droite des
nombres ne convient pas. Imaginons
la suite des nombres 3-adiques avec de plus en plus de chiffres. Ci-contre. |
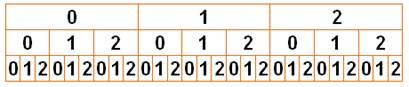
Tous les nombres triadiques à trois
chiffres
|
|
Construction des ensembles de nombres
|
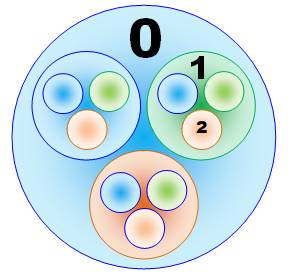
La
première bulle représente le premier chiffre (ici le 0). Les
bulles emboitées représentent les chiffres suivants. L'illustration
montre le nombre triadique 012. |
|
|
Autres exemples: Qu'est-ce
que les nombres p-adiques – Alain M. Robert
|
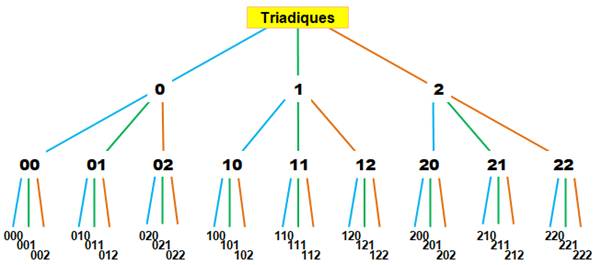
Arbre à trois branches successives. En p-adique, on remonte les branches. Ainsi les trois nombres au centre se lisent: …011 …111 …211 On poursuit l'arbre en ajoutant un étage de branches
ou des chiffres vers la gauche des nombres. |
La distance p-adique est très curieuse ! Prenons deux nombres en bout de branches: …000 et
…001, ils ont en commun 00. La distance entre eux est égale à 1/3². Autres exemples: Distance entre …000 et …002 = 1/32 =
1/9 Distance entre …000 et …020 = 1/31 =
1/3 Distance entre …000 et …222 = 1/30 = 1 |
|
|
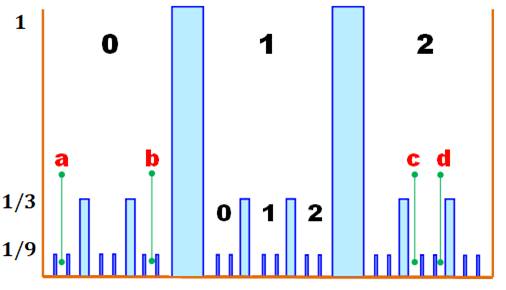
On creuse trois puits numérotés 0, 1et 2.. Les hauteurs sont divisées par 3 à chaque fois.
Même chose pour les largeurs. La distance entre deux nombres est la hauteur de
la plus grande tour qui les sépare.
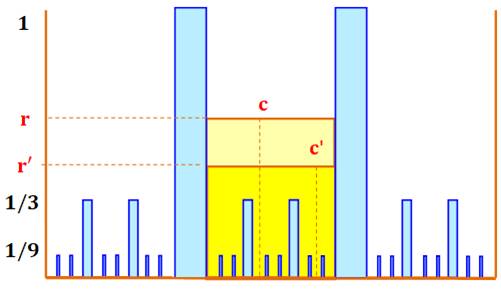
Géométrie déroutante En jaune, on a représenté un cercle: lieu des
points à une distance r de c. En p-adique tous les points situés sur la ligne
du bas sont à la distance 1/3. Ce sont bien les points du cercle p-adique. Imaginons un autre cercle de rayon r' < r et
de centre c' voisin de c. Ce deuxième cercle est inclus dans le
premier ou égal au premier, mais
jamais en intersection. |
Représentation des triadiques en
puits et tours
Représentation de deux cercles
p-adiques
|
|
Voir Fractales
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |