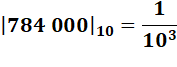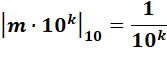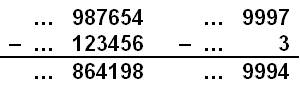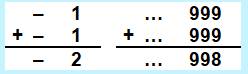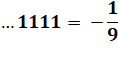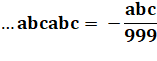|
Édition du: 02/10/2022 |
Faites un double-clic pour un retour en haut de page
![]()
|
NOMBRES décadiques ou 10-adique ou BRENOMS Nombres
p-adique à base 10. Ce sont nos nombres ordinaires, mais avec inversion des
limites de droite à gauche. Un nombre ordinaire se poursuit à l'infini à droite.
Les décadiques, c'est l'inverse: ils se poursuivent à l'infini à gauche. Cette
inversion est propice à résoudre de nombreux problèmes en théorie des nombres
(propriétés des racines des polynômes). Un nombre
décadique n'est pas à proprement parler un nombre p-adique où p est un nombre
premier. Leur étude permet de se familiariser avec la notion de nombre
p-adiques. |
||
|
|
Sommaire de cette page >>> Approche >>> Un exemple naturel de nombre décadique >>> Proximité entre nombre décadiques >>> Calculs avec les nombres décadiques >>> Calculs bizarres |
Débutants Glossaire |
|
Idée originale ! Les nombres décadiques sont les nombres ordinaires
vus à l'envers: ce sont les chiffres de gauche (poids forts) qui se
prolongent. |
…9876 est
p-adique. …333,0
est p-adique périodique; le 3 se répètent indéfiniment à gauche. |
|
|
Le p de p-adique Normalement le p est un nombre premier. Les
nombres sont écrits en base de numération p (si p = 5, seuls les chiffres 0,
1, 2, 3, 4 sont admis). Les nombres décadiques ou 10-adiques font
exception (10 n'est pas premier), mais leur étude constitue une approche plus
sympathique de ces nombres étranges. |
…54321
est p-adique avec p = 5 ou plus. …98765
est "p-adique" avec p = 10 ou plus. |
|
|
On va développer une idée simple qui nous conduira à
inventer deux nombres décadiques naturels. On va chercher des nombres qui sont leur propre carré en
décadique. On rappelle que, si le plus grand opérande comporte k
chiffres, le résultat de l'opération est limité à k chiffres en 10-adique.
Ex: 98 + 10 = 08; 99 + 1 = 00. |
||
|
Une équation et ses solutions On résout facilement cette équation en
factorisant. Il suffit qu'un des facteurs soit nul pour
que le binôme soit égal à zéro. |
|
|
|
Une curieuse manière de voir
cette équation Imaginons qu'il existe un nombre x tel que
x² = x. Dans ce cas, on montre que: 1 – x est aussi
une solution. |
|
|
|
Une non moins curieuse
conséquence ! Deux nombres non-nuls
et pourtant leur produit est nul. Ces nombres sont des diviseurs de zéro. |
|
|
|
Un exemple Pour info, le produit de nombres
ordinaires. Puis avec des nombres spéciaux (nombres
décadiques), nombres pour lesquels on ne conserve pas plus de chiffres que
dans les opérandes. Ce produit continue à l'infini en ajoutant
des chiffres à gauche. |
376
× 625 = 250 000 …376
× …625 = …000 …9376
× …0625 = …0000 …09376
× …90625 = …00000 etc. |
|
Suite: Nombres
p-adiques et nombres automorphes
Voir Solution des équations
/ Nombres
automorphes
|
Pourquoi 0,333… = 1/3 En fait, 0,333… est une notation raccourcie pour
une suite infinie. On montre (suite de
Cauchy) que cette suite converge vers
1/3. On dit que cette suite conduit à des nombres de
plus en plus proches de 1/3. Qu'est-ce que cela veut dire ? |
|
||
|
Métrique ordinaire Deux nombres sont proches si la valeur absolue de leur différence est
faible. C'est la distance
définie par la valeur absolue de la différence. On parle ici de métrique et, on va
définir une métrique différente pour les nombres p-adiques. |
Métrique ordinaire
Métrique décadique
|
||
|
Métrique décadique Deux nombres décadiques sont proches s'ils se ressemblent par leurs
chiffres finaux (unités, dizaines …). Leur différence présente de nombreux zéros à droite. |
789 321 et 5 321 sont proches Car: 789 321 – 5 321 = 784 000 |
||
|
Définition Comment formuler ce type de proximité ? On cherche le coefficient m qui est le plus grand nombre non-divisible
par 10. Ainsi, deux nombres décadiques sont proches si leur différence
décadique est petite. |
784 000 = 784 · 103 m = 784 et k = 3 d10 (784
000) = 1/ 103 = 10-3 Notation
Exemple |1000|10 =
|55000|10 = |99000|10 =
1/1000 |
||
|
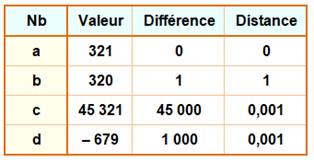
Exemples Voyez comme la distance décadique est contre-intuitive. Il se peut que la distance ordinaire entre deux nombres soit très
grande, alors que celle décadique est faible. Encore plus étrange avec les nombres négatifs: ici la différence se
note bien: 321 – (–679) = 1000. |
Par rapport à 321
|
||
|
Addition C'est tout simplement une addition classique en
tenant compte des retenues. La différence: on stoppe les chiffres à droite au
niveau de ceux des opérandes. Notez les bizarreries qui apparaissent avec
l'addition qui figure à droite (somme nulle). |
|
|
|
Soustraction Exactement la même procédure. Vérification en ajoutant les deux derniers pour
retrouver le premier. |
|
|
|
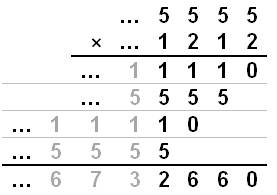
Multiplication Ces multiplications entre nombres décadiques et nombres ordinaires
sont possibles, mais à prendre avec prudence: on note (opération à
droite) que l'écriture de 1/3 en décadique évoque fortement celle de 2/3 en
nombres réels. 1/3 =
…666710D alors qu'en nombres réels: 2/3 =
0,666…10 (parfois arrondi à 0,667). La multiplication du bas entre décadiques est réalisée comme une multiplication
ordinaire. Comme d'habitude en décadique, les chiffres de
gauche qui dépassent la quantité de chiffres des opérandes sont ignorés. Ainsi 5555 × 1212 = 2660 en décadique, des nombres entiers |
|
|
|
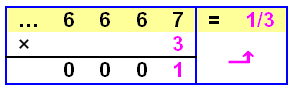
Division et inverse d'un nombre Pas toujours possible avec les décadiques. Par exemple, aucun chiffre x ne peut satisfaire
la multiplication indiquée (5 × a = 1 est impossible). Donc pas d'inverse pour 5. Il existe des cas où, le calcul d'un inverse est
possible (cas de 7), mais pas tout le temps. Pour avoir toute liberté avec la division, il
faudra travailler avec des nombres p-adiques où p est un nombre premier. |
|
|
|
Bizarreries en 9 Quelle est la distance entre 9 et – 1 ? 9 – (–1) = 10.
Et avec 99 ?
99 – (–1) = 100. Et avec 99… 99k ? 99…99k –
(–1) = 10k. Conclusion, plus il y a de 9 plus on se rapproche
de –1. Comme 0,333… = 1/3, on peut dire ici que …999 = –1. Et quid de l'addition de ces deux nombres égaux ?
|
Les
pointillés indiquent que les derniers chiffres se poursuivent sur la gauche. Suite …999 = -1
…998 = -2 …997 = -3 … On note
que les nombres p-adiques négatifs n'ont pas de signe. |
||
|
Calcul d'inverses En multipliant
…1111 (des "1" jusqu'à l'infini) par 9 on obtient – 1 et en
divisant cette expression par 9 on obtient la valeur factionnaire du
décadique …1111 Est-il possible de calculer la valeur décadique
de 1/9 ? En complétant l'addition de gauche, on trouve que
1/9 = … 8889 (des 8 jusqu'à l'infini). Facile ! Mais voyez l'addition de droite. 8/9 est
obtenu en multipliant …1111 par 8.
Nous avons donc …8889 qui représente 1/9, et – 8/9 représenté par
…8888. Avec une unité de différence, le nombre
décadique devient positif ou négatif.
Notez au passage que, de fait, le signe moins est inutile en
décadique. Voyez comment vérifier que …6667 = 1/3
|
9 × …1111 = …9999 = –1
|
||
|
Conversion d'un décadique
périodique La procédure est du même type que celle utilisée
pour les nombres
périodiques ordinaires: multiplication par une puissance de 10 et
soustraction. … 343434 = –
34/99 Et en général
|
|
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |