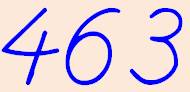Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 06/07/2023 M'écrire Brèves de Maths

Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	0 / 0,… / 1 / 10 / 50 / 100 / 200 / 300			400 à 499		500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100
	400	410	420	430	440	450	460	470	480	490
	460	461	462	463	464	465	466	467	468	469

Quatre-cent-soixante-trois

Four hundred sixty-three

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1 1100 1111
Bases	7178 11121
Romain	CD LX III

Suite

Congruent

Déficient

Élégant

Hogben

Impair

Premier de Luhn

Premier jumeau (avec 461)

Géométrique

Heptagonal centré (12^e)

Chiffres et numération

463 + (4×6×3) = 535 463 – 364 = 99

Devient palindrome en ajoutant le produit de ses chiffres et repdigit en lui retirant son retourné.

Addition et soustraction

463 = 53 + 59 + 61 + 67 + 71 + 73 + 79	Somme de nombres premiers consécutifs.
463 = (ab + bc + ca) 463 = 1 x3 + 3x115 + 115x1 463 = 1x7 + 7x57 + 57x1 463 = 1x15 + 15x28 + 28x1 463 = 3x5 + 5x56 + 56x 3 463 = 7x9 + 9x25 + 25x7 463 = 8x9 + 9x23 + 23x8	Il est possible d'obtenir ce nombre avec cette formule pour des valeurs entières de a, b et c. Tous les nombres plus grands sont accessibles avec cette formule et souvent de très nombreuses fois. Il y a 18 nombres inférieurs qui ne sont pas accessibles avec cette formule dont le plus grand est 462.

Multiplication, division, diviseurs

{463, 467, 479, 487, 491, 499, 503} mod 4 = 3

Ces sept nombres premiers sont en 4n + 3. Plus petite telle configuration. Pour quatre premiers: 199, 211, 223, 227. Pour huit premiers: 36551, 36559, 36563, 36571, 36583, 36587, 36599, 36607.

Avec les puissances

463 = 10² + 3 × 11²	Une des sommes de quatre carrés >>>
463 = 7² + 8² + 9² + 10² + 13²	Somme de carrés.
463 = 2^2 + 6^3 + 3^5	Nombre élégant: somme de ses chiffres en puissance.

En puissances

6 = 5^4 × 7^3 – 463^2 = 214 375 – 214 369

Expression du nombre 6 en différence de deux nombres puissants. W. Narkiewicz et S.W. Golomb

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 1, 0, 0, 1, 1, 1, 1] 3, [1, 2, 2, 0, 1, 1] 4, [1, 3, 0, 3, 3] 5, [3, 3, 2, 3] 6, [2, 0, 5, 1] 7, [1, 2, 3, 1] 8, [7, 1, 7] 9, [5, 6, 4] 10, [4, 6, 3] 11, [3, 9, 1]	12, [3, 2, 7] 13, [2, 9, 8] 14, [2, 5, 1] 15, [2, 0, 13] 16, [1, 12, 15] 17, [1, 10, 4] 18, [1, 7, 13] 19, [1, 5, 7] 20, [1, 3, 3] 21, [1, 1, 1]	22, [21, 1] 23, [20, 3] 24, [19, 7] 25, [18, 13] 26, [17, 21] 27, [17, 4] 28, [16, 15] 29, [15, 28] 30, [15, 13] 60, [7, 43]	21, [1, 1, 1] 462, [1, 1]

Voir Bases / Brésiliens

Retour Suite	Nombres en 450 Nombres en 470
Voir	Nom des nombres Nombres géométriques
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres

Cette page

http://villemin.gerard.free.fr/NombDico/N100a500/Nomb400/Nb463.htm